A simple and provable algorithm for sparse diagonal CCA

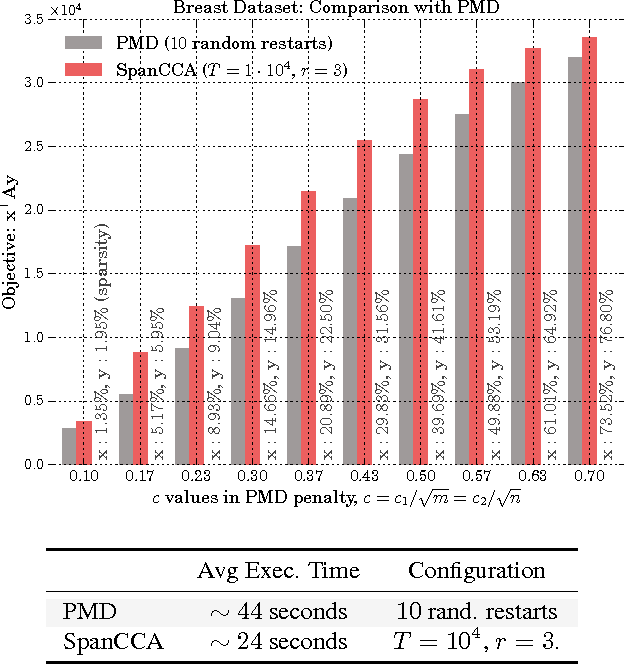
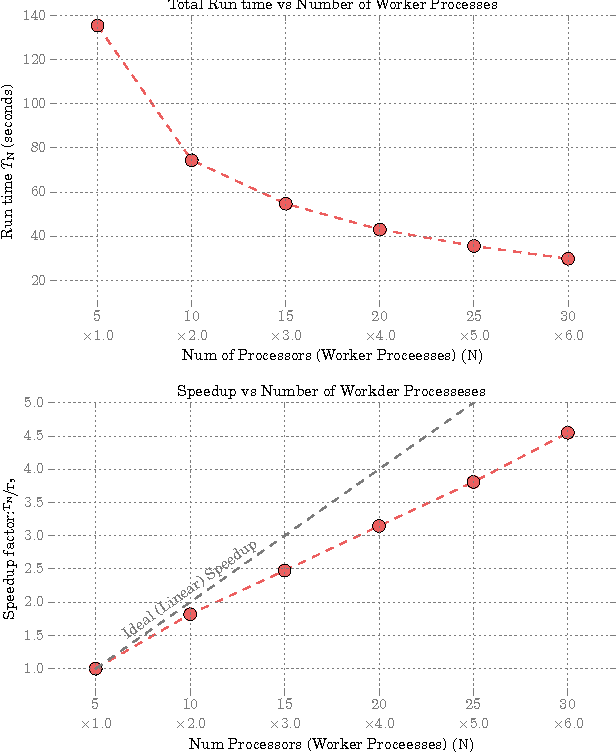
Given two sets of variables, derived from a common set of samples, sparse Canonical Correlation Analysis (CCA) seeks linear combinations of a small number of variables in each set, such that the induced canonical variables are maximally correlated. Sparse CCA is NP-hard. We propose a novel combinatorial algorithm for sparse diagonal CCA, i.e., sparse CCA under the additional assumption that variables within each set are standardized and uncorrelated. Our algorithm operates on a low rank approximation of the input data and its computational complexity scales linearly with the number of input variables. It is simple to implement, and parallelizable. In contrast to most existing approaches, our algorithm administers precise control on the sparsity of the extracted canonical vectors, and comes with theoretical data-dependent global approximation guarantees, that hinge on the spectrum of the input data. Finally, it can be straightforwardly adapted to other constrained variants of CCA enforcing structure beyond sparsity. We empirically evaluate the proposed scheme and apply it on a real neuroimaging dataset to investigate associations between brain activity and behavior measurements.

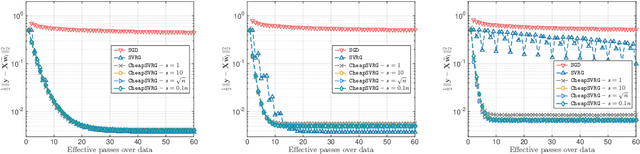
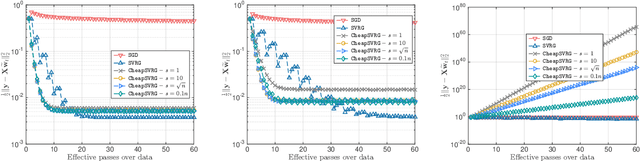
Trading-off variance and complexity in stochastic gradient descent

Stochastic gradient descent is the method of choice for large-scale machine learning problems, by virtue of its light complexity per iteration. However, it lags behind its non-stochastic counterparts with respect to the convergence rate, due to high variance introduced by the stochastic updates. The popular Stochastic Variance-Reduced Gradient (SVRG) method mitigates this shortcoming, introducing a new update rule which requires infrequent passes over the entire input dataset to compute the full-gradient. In this work, we propose CheapSVRG, a stochastic variance-reduction optimization scheme. Our algorithm is similar to SVRG but instead of the full gradient, it uses a surrogate which can be efficiently computed on a small subset of the input data. It achieves a linear convergence rate ---up to some error level, depending on the nature of the optimization problem---and features a trade-off between the computational complexity and the convergence rate. Empirical evaluation shows that CheapSVRG performs at least competitively compared to the state of the art.

Bipartite Correlation Clustering -- Maximizing Agreements

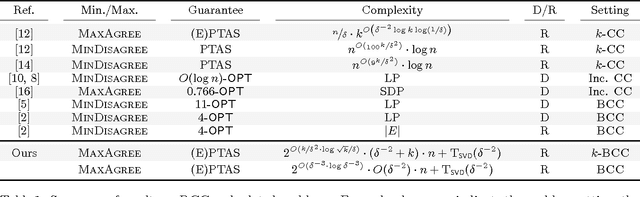
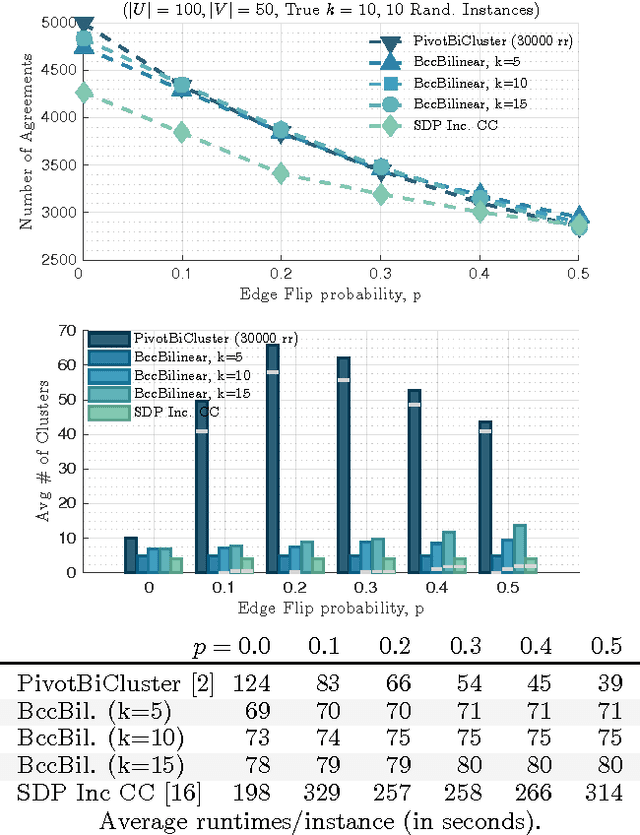
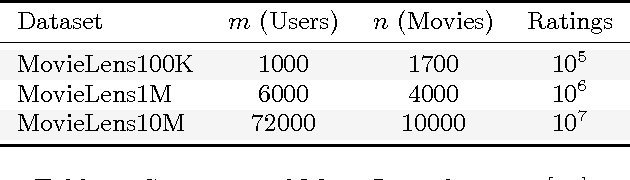
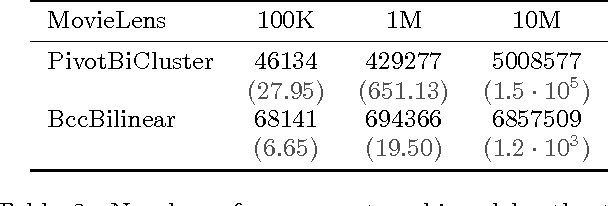
In Bipartite Correlation Clustering (BCC) we are given a complete bipartite graph $G$ with `+' and `-' edges, and we seek a vertex clustering that maximizes the number of agreements: the number of all `+' edges within clusters plus all `-' edges cut across clusters. BCC is known to be NP-hard. We present a novel approximation algorithm for $k$-BCC, a variant of BCC with an upper bound $k$ on the number of clusters. Our algorithm outputs a $k$-clustering that provably achieves a number of agreements within a multiplicative ${(1-\delta)}$-factor from the optimal, for any desired accuracy $\delta$. It relies on solving a combinatorially constrained bilinear maximization on the bi-adjacency matrix of $G$. It runs in time exponential in $k$ and $\delta^{-1}$, but linear in the size of the input. Further, we show that, in the (unconstrained) BCC setting, an ${(1-\delta)}$-approximation can be achieved by $O(\delta^{-1})$ clusters regardless of the size of the graph. In turn, our $k$-BCC algorithm implies an Efficient PTAS for the BCC objective of maximizing agreements.

Sparse PCA via Bipartite Matchings

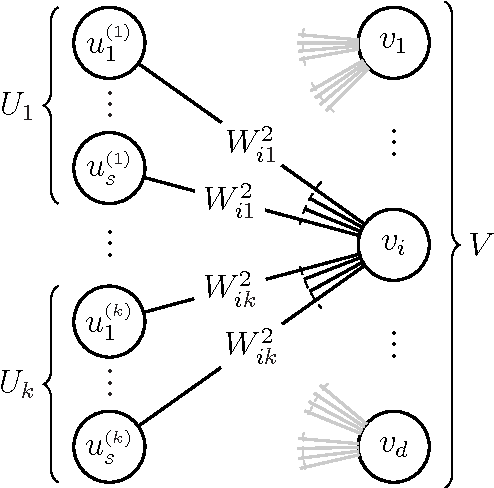
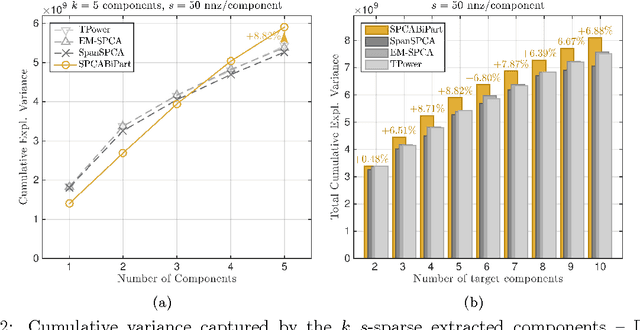
We consider the following multi-component sparse PCA problem: given a set of data points, we seek to extract a small number of sparse components with disjoint supports that jointly capture the maximum possible variance. These components can be computed one by one, repeatedly solving the single-component problem and deflating the input data matrix, but as we show this greedy procedure is suboptimal. We present a novel algorithm for sparse PCA that jointly optimizes multiple disjoint components. The extracted features capture variance that lies within a multiplicative factor arbitrarily close to 1 from the optimal. Our algorithm is combinatorial and computes the desired components by solving multiple instances of the bipartite maximum weight matching problem. Its complexity grows as a low order polynomial in the ambient dimension of the input data matrix, but exponentially in its rank. However, it can be effectively applied on a low-dimensional sketch of the data; this allows us to obtain polynomial-time approximation guarantees via spectral bounds. We evaluate our algorithm on real data-sets and empirically demonstrate that in many cases it outperforms existing, deflation-based approaches.

Stay on path: PCA along graph paths

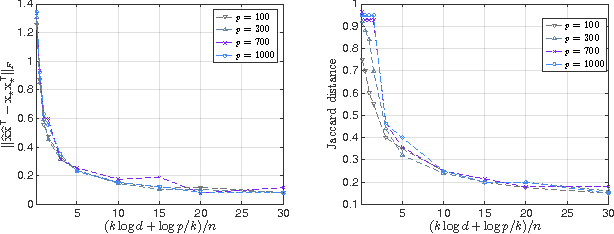
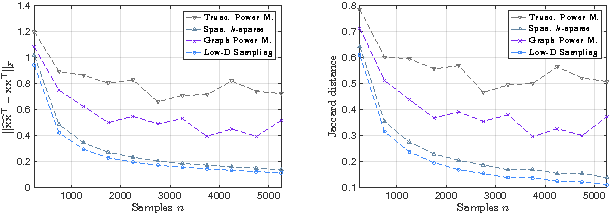
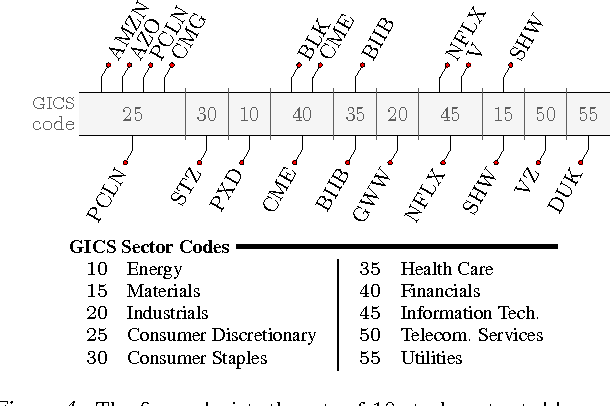
We introduce a variant of (sparse) PCA in which the set of feasible support sets is determined by a graph. In particular, we consider the following setting: given a directed acyclic graph $G$ on $p$ vertices corresponding to variables, the non-zero entries of the extracted principal component must coincide with vertices lying along a path in $G$. From a statistical perspective, information on the underlying network may potentially reduce the number of observations required to recover the population principal component. We consider the canonical estimator which optimally exploits the prior knowledge by solving a non-convex quadratic maximization on the empirical covariance. We introduce a simple network and analyze the estimator under the spiked covariance model. We show that side information potentially improves the statistical complexity. We propose two algorithms to approximate the solution of the constrained quadratic maximization, and recover a component with the desired properties. We empirically evaluate our schemes on synthetic and real datasets.

The Sparse Principal Component of a Constant-rank Matrix

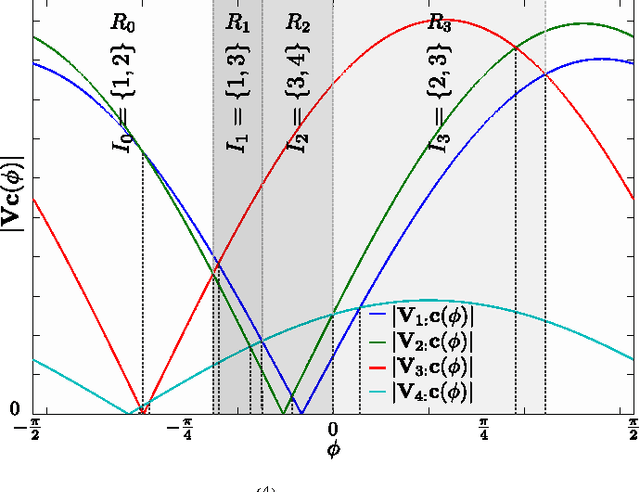
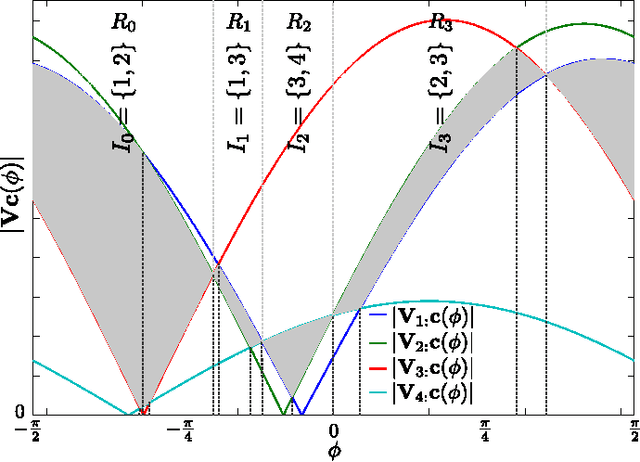
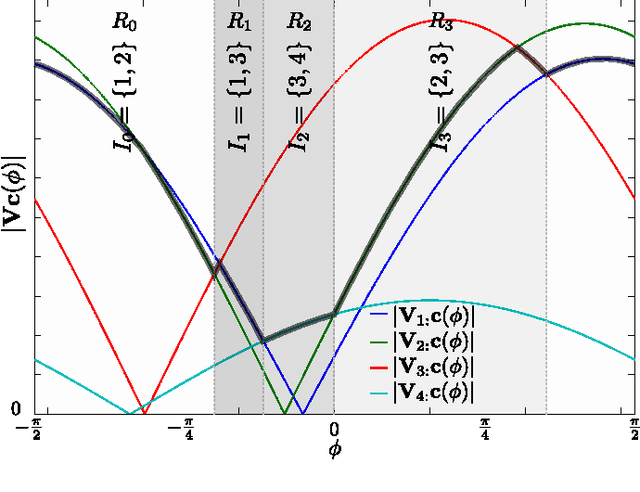
The computation of the sparse principal component of a matrix is equivalent to the identification of its principal submatrix with the largest maximum eigenvalue. Finding this optimal submatrix is what renders the problem ${\mathcal{NP}}$-hard. In this work, we prove that, if the matrix is positive semidefinite and its rank is constant, then its sparse principal component is polynomially computable. Our proof utilizes the auxiliary unit vector technique that has been recently developed to identify problems that are polynomially solvable. Moreover, we use this technique to design an algorithm which, for any sparsity value, computes the sparse principal component with complexity ${\mathcal O}\left(N^{D+1}\right)$, where $N$ and $D$ are the matrix size and rank, respectively. Our algorithm is fully parallelizable and memory efficient.

Sparse Principal Component of a Rank-deficient Matrix

We consider the problem of identifying the sparse principal component of a rank-deficient matrix. We introduce auxiliary spherical variables and prove that there exists a set of candidate index-sets (that is, sets of indices to the nonzero elements of the vector argument) whose size is polynomially bounded, in terms of rank, and contains the optimal index-set, i.e. the index-set of the nonzero elements of the optimal solution. Finally, we develop an algorithm that computes the optimal sparse principal component in polynomial time for any sparsity degree.