Sparse PCA through Low-rank Approximations

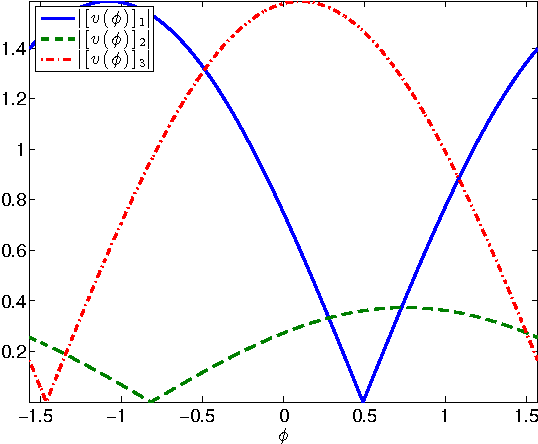
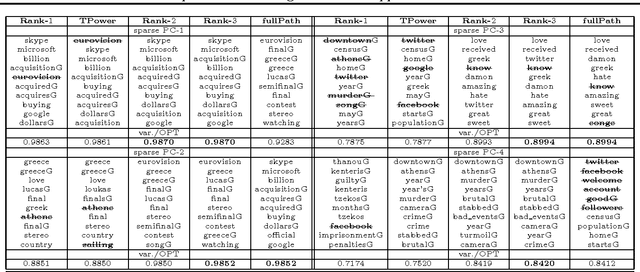
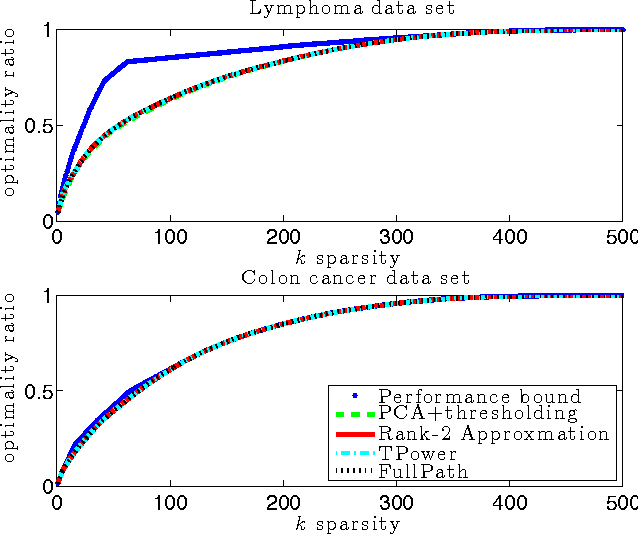
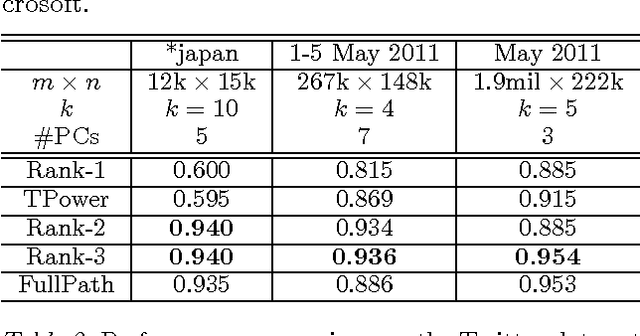
We introduce a novel algorithm that computes the $k$-sparse principal component of a positive semidefinite matrix $A$. Our algorithm is combinatorial and operates by examining a discrete set of special vectors lying in a low-dimensional eigen-subspace of $A$. We obtain provable approximation guarantees that depend on the spectral decay profile of the matrix: the faster the eigenvalue decay, the better the quality of our approximation. For example, if the eigenvalues of $A$ follow a power-law decay, we obtain a polynomial-time approximation algorithm for any desired accuracy. A key algorithmic component of our scheme is a combinatorial feature elimination step that is provably safe and in practice significantly reduces the running complexity of our algorithm. We implement our algorithm and test it on multiple artificial and real data sets. Due to the feature elimination step, it is possible to perform sparse PCA on data sets consisting of millions of entries in a few minutes. Our experimental evaluation shows that our scheme is nearly optimal while finding very sparse vectors. We compare to the prior state of the art and show that our scheme matches or outperforms previous algorithms in all tested data sets.

The Sparse Principal Component of a Constant-rank Matrix

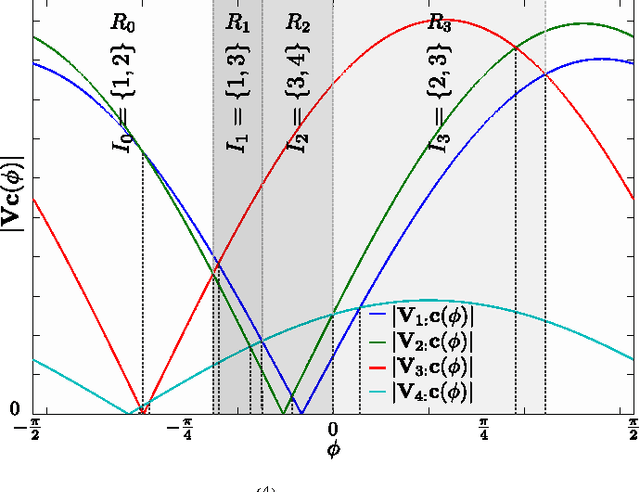
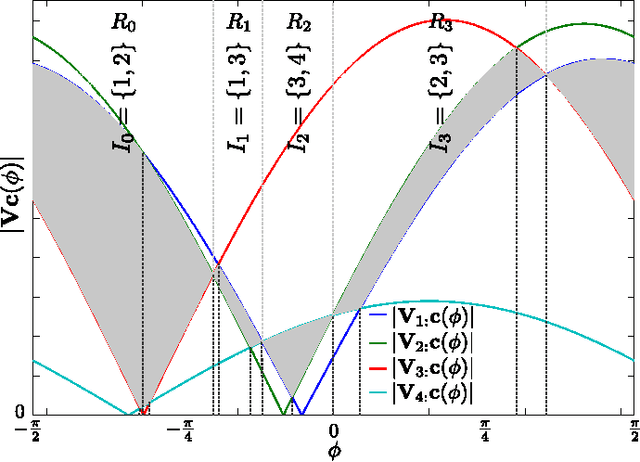
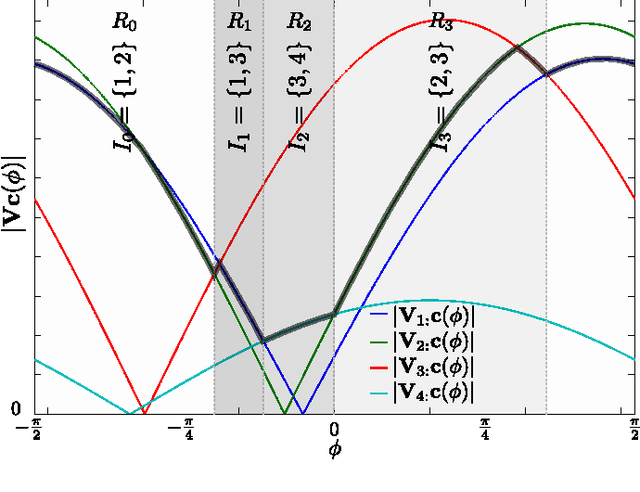
The computation of the sparse principal component of a matrix is equivalent to the identification of its principal submatrix with the largest maximum eigenvalue. Finding this optimal submatrix is what renders the problem ${\mathcal{NP}}$-hard. In this work, we prove that, if the matrix is positive semidefinite and its rank is constant, then its sparse principal component is polynomially computable. Our proof utilizes the auxiliary unit vector technique that has been recently developed to identify problems that are polynomially solvable. Moreover, we use this technique to design an algorithm which, for any sparsity value, computes the sparse principal component with complexity ${\mathcal O}\left(N^{D+1}\right)$, where $N$ and $D$ are the matrix size and rank, respectively. Our algorithm is fully parallelizable and memory efficient.

Sparse Principal Component of a Rank-deficient Matrix

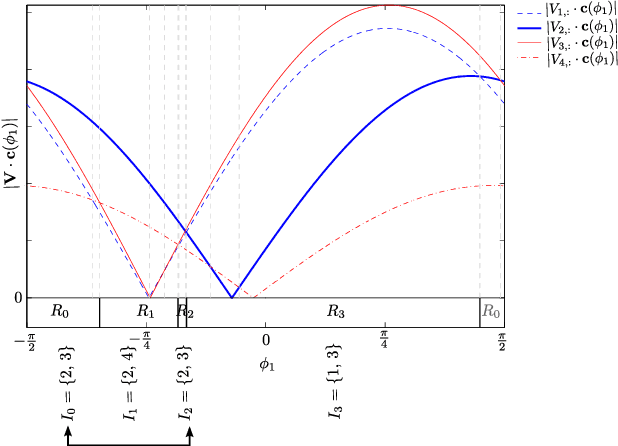
We consider the problem of identifying the sparse principal component of a rank-deficient matrix. We introduce auxiliary spherical variables and prove that there exists a set of candidate index-sets (that is, sets of indices to the nonzero elements of the vector argument) whose size is polynomially bounded, in terms of rank, and contains the optimal index-set, i.e. the index-set of the nonzero elements of the optimal solution. Finally, we develop an algorithm that computes the optimal sparse principal component in polynomial time for any sparsity degree.