The Sparse Principal Component of a Constant-rank Matrix

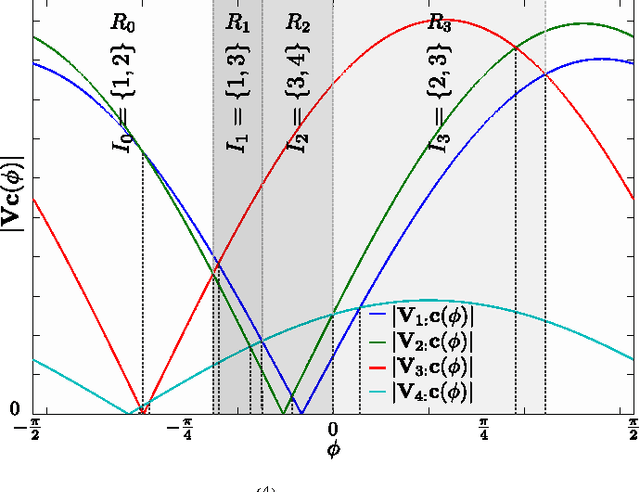
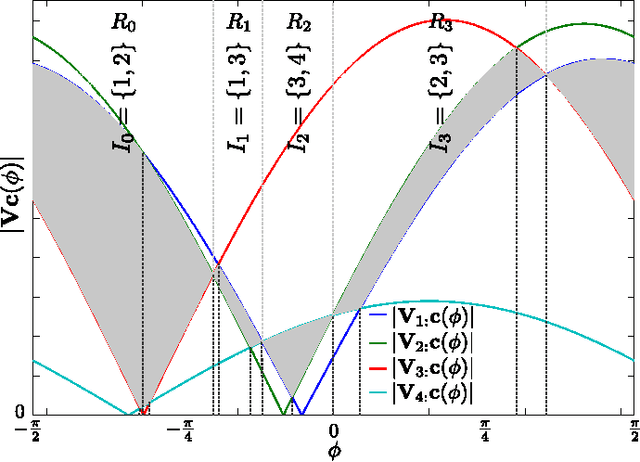
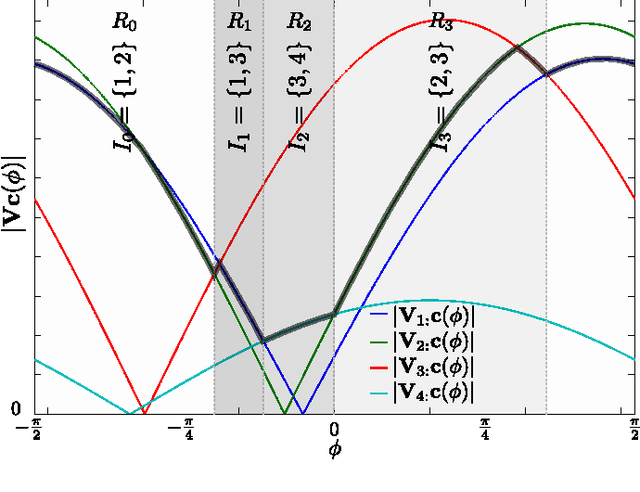
The computation of the sparse principal component of a matrix is equivalent to the identification of its principal submatrix with the largest maximum eigenvalue. Finding this optimal submatrix is what renders the problem ${\mathcal{NP}}$-hard. In this work, we prove that, if the matrix is positive semidefinite and its rank is constant, then its sparse principal component is polynomially computable. Our proof utilizes the auxiliary unit vector technique that has been recently developed to identify problems that are polynomially solvable. Moreover, we use this technique to design an algorithm which, for any sparsity value, computes the sparse principal component with complexity ${\mathcal O}\left(N^{D+1}\right)$, where $N$ and $D$ are the matrix size and rank, respectively. Our algorithm is fully parallelizable and memory efficient.

Some Options for L1-Subspace Signal Processing

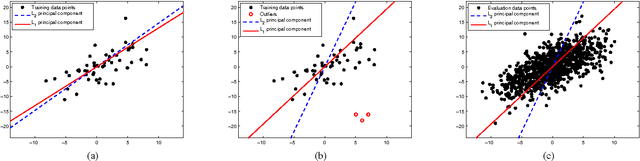
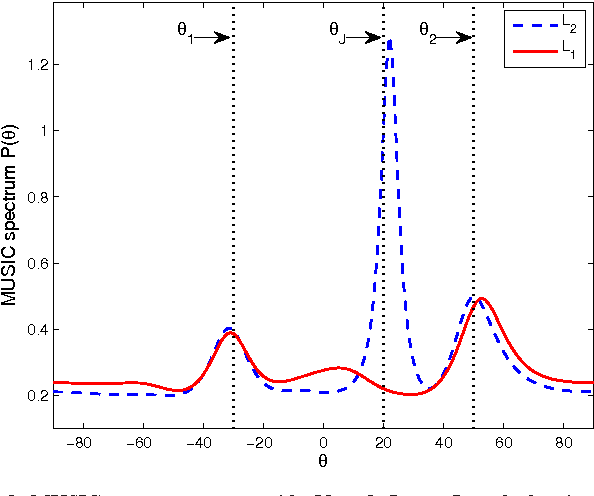
We describe ways to define and calculate $L_1$-norm signal subspaces which are less sensitive to outlying data than $L_2$-calculated subspaces. We focus on the computation of the $L_1$ maximum-projection principal component of a data matrix containing N signal samples of dimension D and conclude that the general problem is formally NP-hard in asymptotically large N, D. We prove, however, that the case of engineering interest of fixed dimension D and asymptotically large sample support N is not and we present an optimal algorithm of complexity $O(N^D)$. We generalize to multiple $L_1$-max-projection components and present an explicit optimal $L_1$ subspace calculation algorithm in the form of matrix nuclear-norm evaluations. We conclude with illustrations of $L_1$-subspace signal processing in the fields of data dimensionality reduction and direction-of-arrival estimation.

Sparse Principal Component of a Rank-deficient Matrix

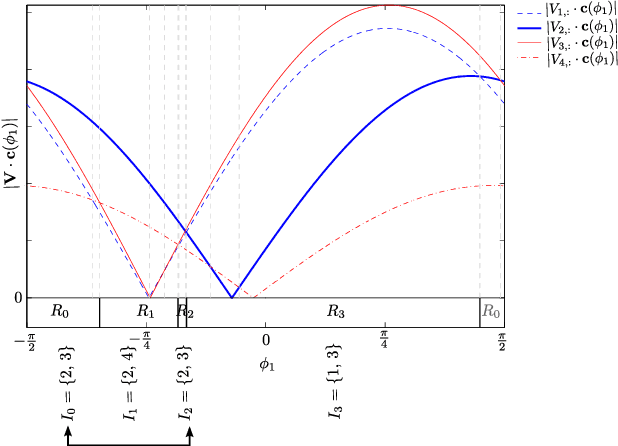
We consider the problem of identifying the sparse principal component of a rank-deficient matrix. We introduce auxiliary spherical variables and prove that there exists a set of candidate index-sets (that is, sets of indices to the nonzero elements of the vector argument) whose size is polynomially bounded, in terms of rank, and contains the optimal index-set, i.e. the index-set of the nonzero elements of the optimal solution. Finally, we develop an algorithm that computes the optimal sparse principal component in polynomial time for any sparsity degree.