Some Options for L1-Subspace Signal Processing
Paper and Code
Sep 04, 2013
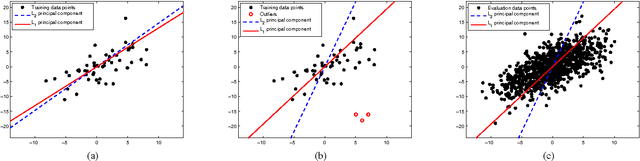
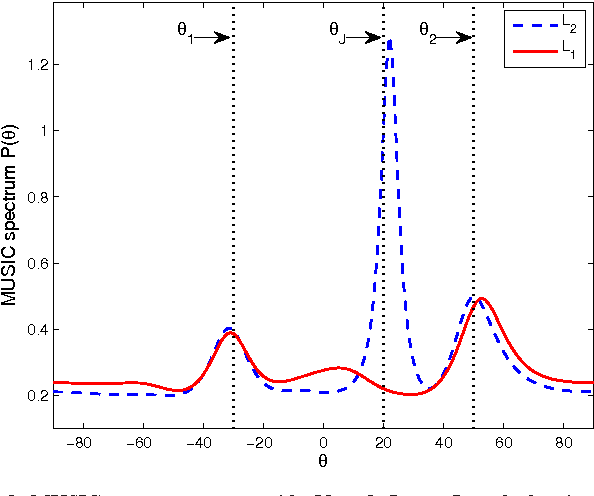
We describe ways to define and calculate $L_1$-norm signal subspaces which are less sensitive to outlying data than $L_2$-calculated subspaces. We focus on the computation of the $L_1$ maximum-projection principal component of a data matrix containing N signal samples of dimension D and conclude that the general problem is formally NP-hard in asymptotically large N, D. We prove, however, that the case of engineering interest of fixed dimension D and asymptotically large sample support N is not and we present an optimal algorithm of complexity $O(N^D)$. We generalize to multiple $L_1$-max-projection components and present an explicit optimal $L_1$ subspace calculation algorithm in the form of matrix nuclear-norm evaluations. We conclude with illustrations of $L_1$-subspace signal processing in the fields of data dimensionality reduction and direction-of-arrival estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge