Convolutional Neural Network Compression via Dynamic Parameter Rank Pruning

While Convolutional Neural Networks (CNNs) excel at learning complex latent-space representations, their over-parameterization can lead to overfitting and reduced performance, particularly with limited data. This, alongside their high computational and memory demands, limits the applicability of CNNs for edge deployment. Low-rank matrix approximation has emerged as a promising approach to reduce CNN parameters, but its application presents challenges including rank selection and performance loss. To address these issues, we propose an efficient training method for CNN compression via dynamic parameter rank pruning. Our approach integrates efficient matrix factorization and novel regularization techniques, forming a robust framework for dynamic rank reduction and model compression. We use Singular Value Decomposition (SVD) to model low-rank convolutional filters and dense weight matrices and we achieve model compression by training the SVD factors with back-propagation in an end-to-end way. We evaluate our method on an array of modern CNNs, including ResNet-18, ResNet-20, and ResNet-32, and datasets like CIFAR-10, CIFAR-100, and ImageNet (2012), showcasing its applicability in computer vision. Our experiments show that the proposed method can yield substantial storage savings while maintaining or even enhancing classification performance.

The Exact Solution to Rank-1 L1-norm TUCKER2 Decomposition

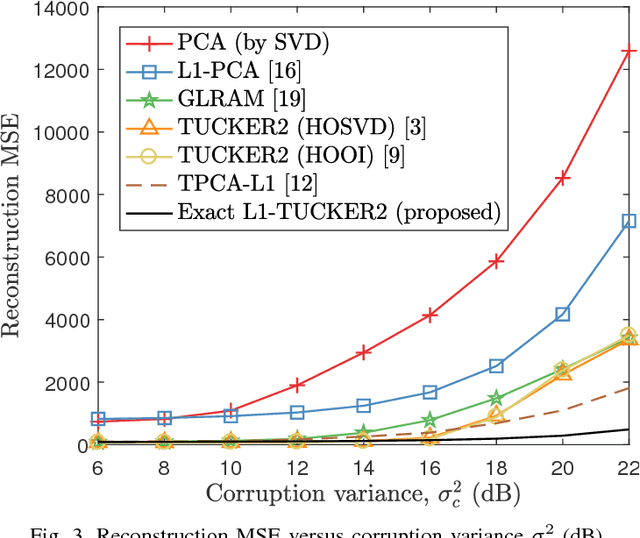
We study rank-1 {L1-norm-based TUCKER2} (L1-TUCKER2) decomposition of 3-way tensors, treated as a collection of $N$ $D \times M$ matrices that are to be jointly decomposed. Our contributions are as follows. i) We prove that the problem is equivalent to combinatorial optimization over $N$ antipodal-binary variables. ii) We derive the first two algorithms in the literature for its exact solution. The first algorithm has cost exponential in $N$; the second one has cost polynomial in $N$ (under a mild assumption). Our algorithms are accompanied by formal complexity analysis. iii) We conduct numerical studies to compare the performance of exact L1-TUCKER2 (proposed) with standard HOSVD, HOOI, GLRAM, PCA, L1-PCA, and TPCA-L1. Our studies show that L1-TUCKER2 outperforms (in tensor approximation) all the above counterparts when the processed data are outlier corrupted.

Efficient L1-Norm Principal-Component Analysis via Bit Flipping

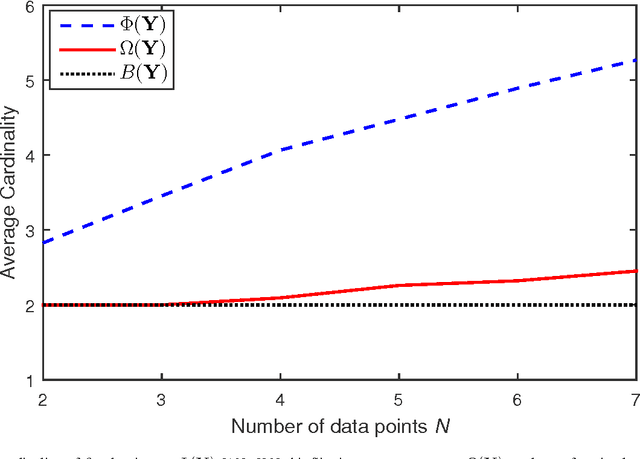
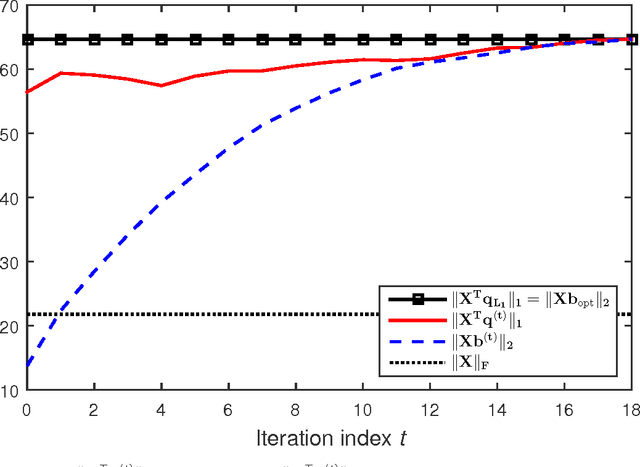
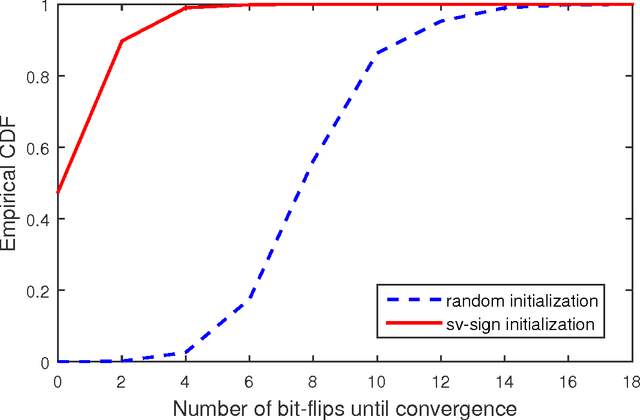
It was shown recently that the $K$ L1-norm principal components (L1-PCs) of a real-valued data matrix $\mathbf X \in \mathbb R^{D \times N}$ ($N$ data samples of $D$ dimensions) can be exactly calculated with cost $\mathcal{O}(2^{NK})$ or, when advantageous, $\mathcal{O}(N^{dK - K + 1})$ where $d=\mathrm{rank}(\mathbf X)$, $K<d$ [1],[2]. In applications where $\mathbf X$ is large (e.g., "big" data of large $N$ and/or "heavy" data of large $d$), these costs are prohibitive. In this work, we present a novel suboptimal algorithm for the calculation of the $K < d$ L1-PCs of $\mathbf X$ of cost $\mathcal O(ND \mathrm{min} \{ N,D\} + N^2(K^4 + dK^2) + dNK^3)$, which is comparable to that of standard (L2-norm) PC analysis. Our theoretical and experimental studies show that the proposed algorithm calculates the exact optimal L1-PCs with high frequency and achieves higher value in the L1-PC optimization metric than any known alternative algorithm of comparable computational cost. The superiority of the calculated L1-PCs over standard L2-PCs (singular vectors) in characterizing potentially faulty data/measurements is demonstrated with experiments on data dimensionality reduction and disease diagnosis from genomic data.

Some Options for L1-Subspace Signal Processing

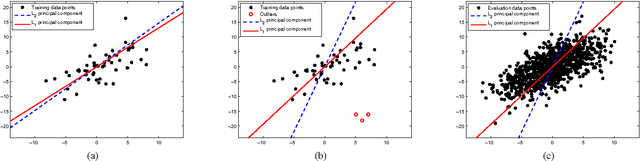
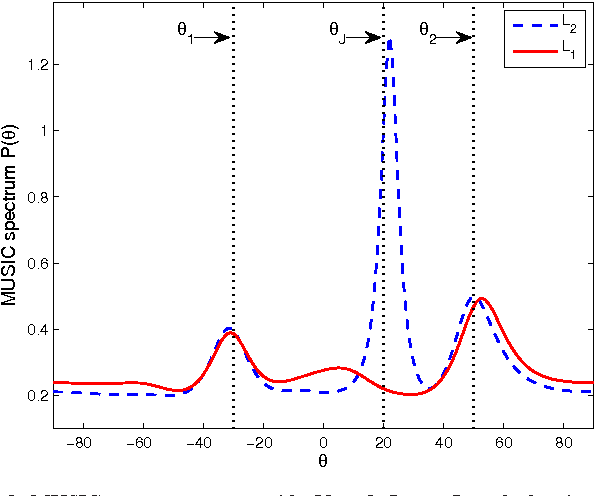
We describe ways to define and calculate $L_1$-norm signal subspaces which are less sensitive to outlying data than $L_2$-calculated subspaces. We focus on the computation of the $L_1$ maximum-projection principal component of a data matrix containing N signal samples of dimension D and conclude that the general problem is formally NP-hard in asymptotically large N, D. We prove, however, that the case of engineering interest of fixed dimension D and asymptotically large sample support N is not and we present an optimal algorithm of complexity $O(N^D)$. We generalize to multiple $L_1$-max-projection components and present an explicit optimal $L_1$ subspace calculation algorithm in the form of matrix nuclear-norm evaluations. We conclude with illustrations of $L_1$-subspace signal processing in the fields of data dimensionality reduction and direction-of-arrival estimation.