Dimitris G. Chachlakis
The Exact Solution to Rank-1 L1-norm TUCKER2 Decomposition
Oct 31, 2017

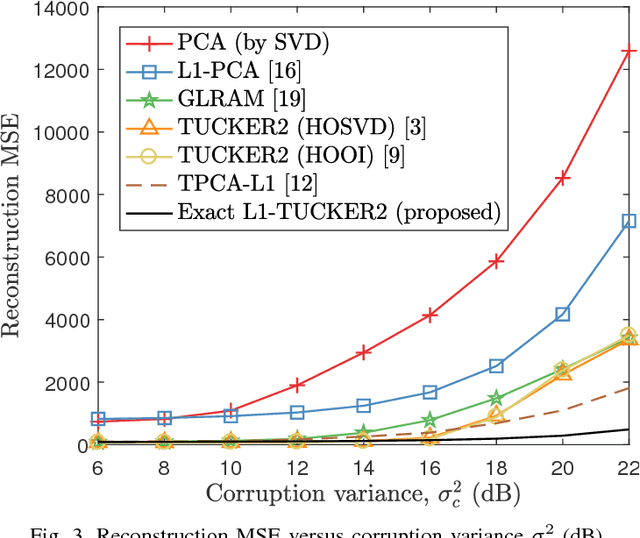
Abstract:We study rank-1 {L1-norm-based TUCKER2} (L1-TUCKER2) decomposition of 3-way tensors, treated as a collection of $N$ $D \times M$ matrices that are to be jointly decomposed. Our contributions are as follows. i) We prove that the problem is equivalent to combinatorial optimization over $N$ antipodal-binary variables. ii) We derive the first two algorithms in the literature for its exact solution. The first algorithm has cost exponential in $N$; the second one has cost polynomial in $N$ (under a mild assumption). Our algorithms are accompanied by formal complexity analysis. iii) We conduct numerical studies to compare the performance of exact L1-TUCKER2 (proposed) with standard HOSVD, HOOI, GLRAM, PCA, L1-PCA, and TPCA-L1. Our studies show that L1-TUCKER2 outperforms (in tensor approximation) all the above counterparts when the processed data are outlier corrupted.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge