NeuroQuery: comprehensive meta-analysis of human brain mapping

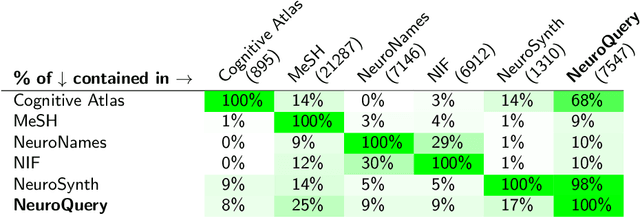
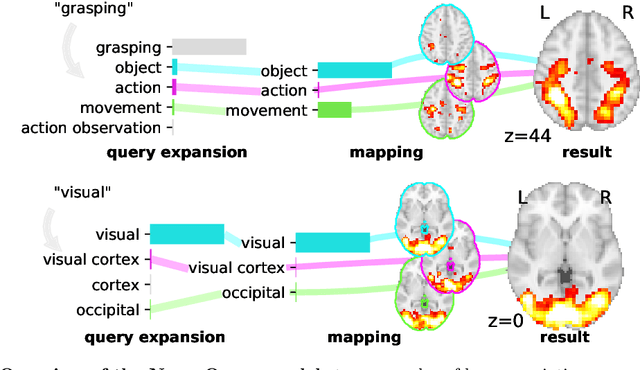
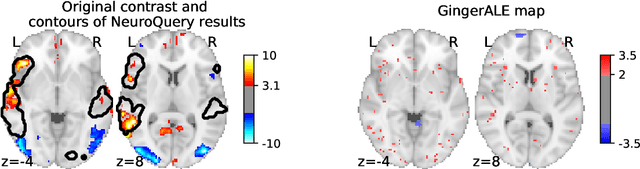
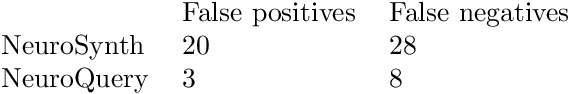
Reaching a global view of brain organization requires assembling evidence on widely different mental processes and mechanisms. The variety of human neuroscience concepts and terminology poses a fundamental challenge to relating brain imaging results across the scientific literature. Existing meta-analysis methods perform statistical tests on sets of publications associated with a particular concept. Thus, large-scale meta-analyses only tackle single terms that occur frequently. We propose a new paradigm, focusing on prediction rather than inference. Our multivariate model predicts the spatial distribution of neurological observations, given text describing an experiment, cognitive process, or disease. This approach handles text of arbitrary length and terms that are too rare for standard meta-analysis. We capture the relationships and neural correlates of 7 547 neuroscience terms across 13 459 neuroimaging publications. The resulting meta-analytic tool, neuroquery.org, can ground hypothesis generation and data-analysis priors on a comprehensive view of published findings on the brain.

Text to brain: predicting the spatial distribution of neuroimaging observations from text reports

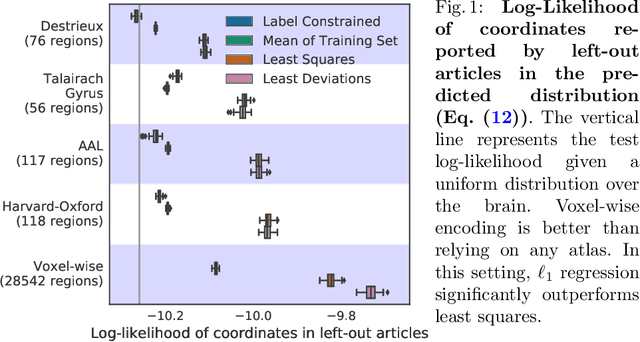
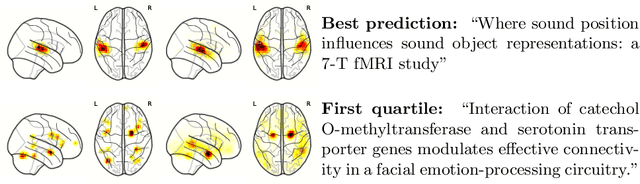
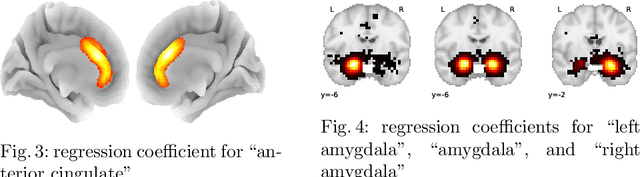
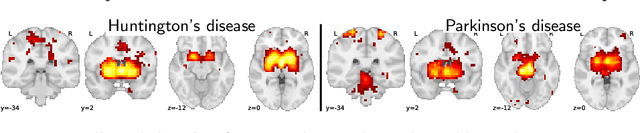
Despite the digital nature of magnetic resonance imaging, the resulting observations are most frequently reported and stored in text documents. There is a trove of information untapped in medical health records, case reports, and medical publications. In this paper, we propose to mine brain medical publications to learn the spatial distribution associated with anatomical terms. The problem is formulated in terms of minimization of a risk on distributions which leads to a least-deviation cost function. An efficient algorithm in the dual then learns the mapping from documents to brain structures. Empirical results using coordinates extracted from the brain-imaging literature show that i) models must adapt to semantic variation in the terms used to describe a given anatomical structure, ii) voxel-wise parameterization leads to higher likelihood of locations reported in unseen documents, iii) least-deviation cost outperforms least-square. As a proof of concept for our method, we use our model of spatial distributions to predict the distribution of specific neurological conditions from text-only reports.

Information Projection and Approximate Inference for Structured Sparse Variables

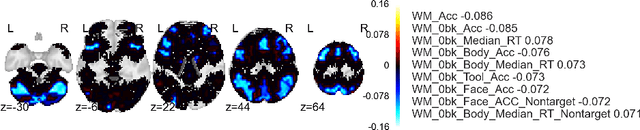
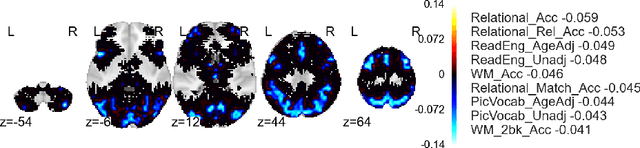
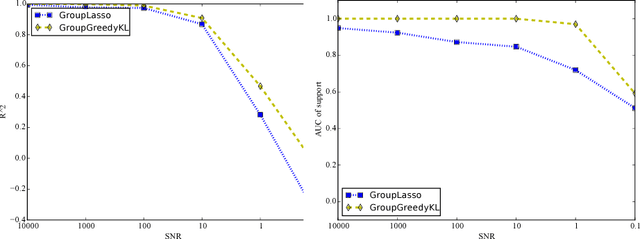
Approximate inference via information projection has been recently introduced as a general-purpose approach for efficient probabilistic inference given sparse variables. This manuscript goes beyond classical sparsity by proposing efficient algorithms for approximate inference via information projection that are applicable to any structure on the set of variables that admits enumeration using a \emph{matroid}. We show that the resulting information projection can be reduced to combinatorial submodular optimization subject to matroid constraints. Further, leveraging recent advances in submodular optimization, we provide an efficient greedy algorithm with strong optimization-theoretic guarantees. The class of probabilistic models that can be expressed in this way is quite broad and, as we show, includes group sparse regression, group sparse principal components analysis and sparse canonical correlation analysis, among others. Moreover, empirical results on simulated data and high dimensional neuroimaging data highlight the superior performance of the information projection approach as compared to established baselines for a range of probabilistic models.

A simple and provable algorithm for sparse diagonal CCA

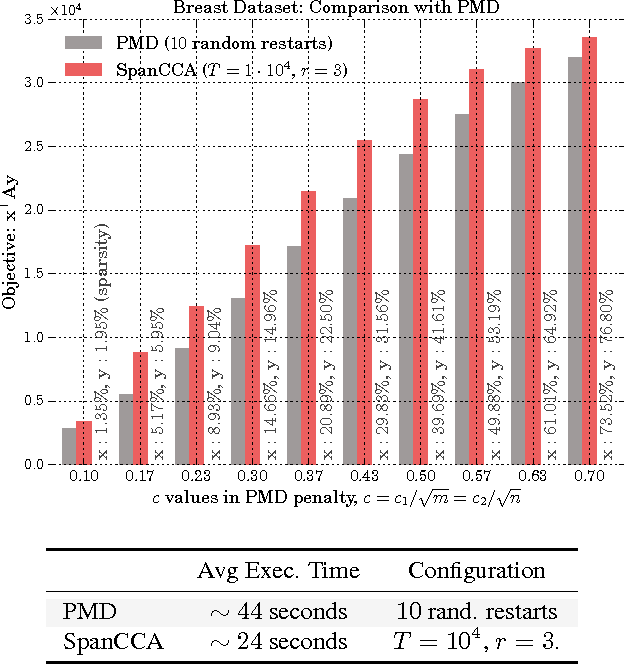
Given two sets of variables, derived from a common set of samples, sparse Canonical Correlation Analysis (CCA) seeks linear combinations of a small number of variables in each set, such that the induced canonical variables are maximally correlated. Sparse CCA is NP-hard. We propose a novel combinatorial algorithm for sparse diagonal CCA, i.e., sparse CCA under the additional assumption that variables within each set are standardized and uncorrelated. Our algorithm operates on a low rank approximation of the input data and its computational complexity scales linearly with the number of input variables. It is simple to implement, and parallelizable. In contrast to most existing approaches, our algorithm administers precise control on the sparsity of the extracted canonical vectors, and comes with theoretical data-dependent global approximation guarantees, that hinge on the spectrum of the input data. Finally, it can be straightforwardly adapted to other constrained variants of CCA enforcing structure beyond sparsity. We empirically evaluate the proposed scheme and apply it on a real neuroimaging dataset to investigate associations between brain activity and behavior measurements.