A simple and provable algorithm for sparse diagonal CCA
Paper and Code
May 29, 2016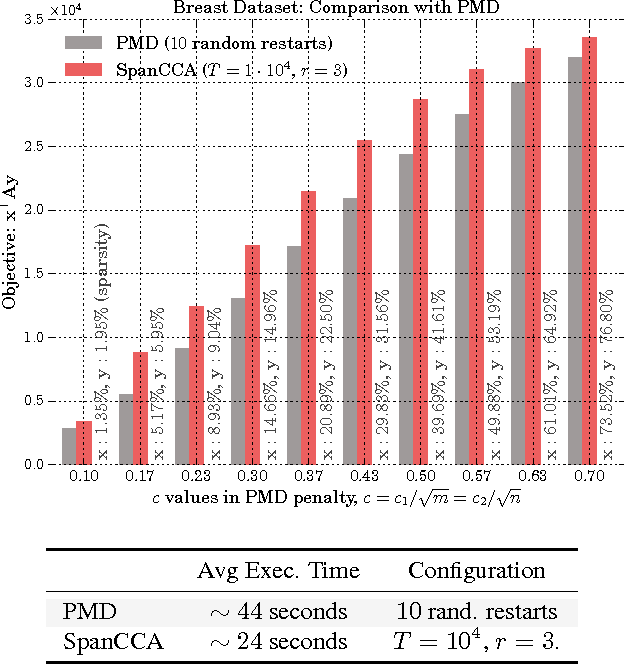

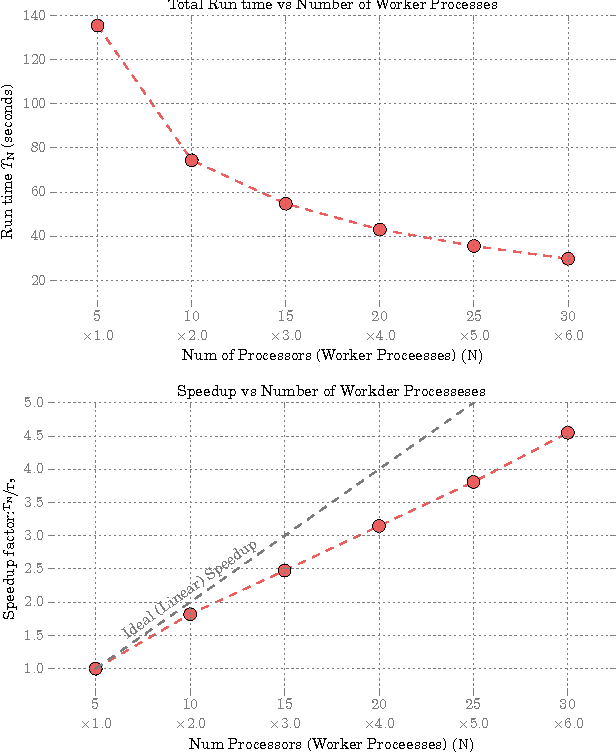
Given two sets of variables, derived from a common set of samples, sparse Canonical Correlation Analysis (CCA) seeks linear combinations of a small number of variables in each set, such that the induced canonical variables are maximally correlated. Sparse CCA is NP-hard. We propose a novel combinatorial algorithm for sparse diagonal CCA, i.e., sparse CCA under the additional assumption that variables within each set are standardized and uncorrelated. Our algorithm operates on a low rank approximation of the input data and its computational complexity scales linearly with the number of input variables. It is simple to implement, and parallelizable. In contrast to most existing approaches, our algorithm administers precise control on the sparsity of the extracted canonical vectors, and comes with theoretical data-dependent global approximation guarantees, that hinge on the spectrum of the input data. Finally, it can be straightforwardly adapted to other constrained variants of CCA enforcing structure beyond sparsity. We empirically evaluate the proposed scheme and apply it on a real neuroimaging dataset to investigate associations between brain activity and behavior measurements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge