Bipartite Correlation Clustering -- Maximizing Agreements
Paper and Code
Mar 09, 2016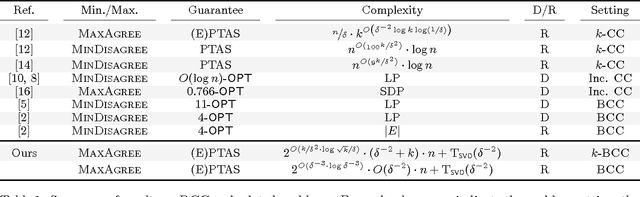
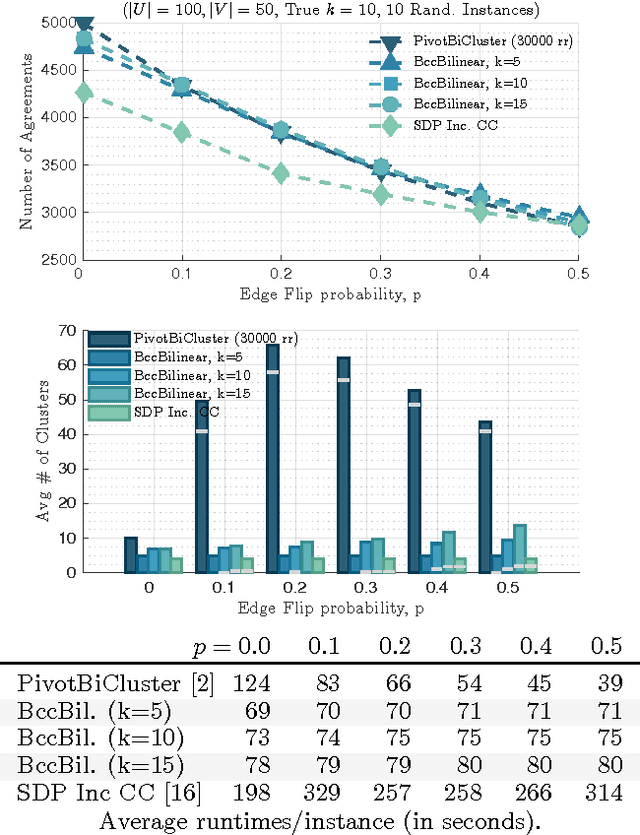
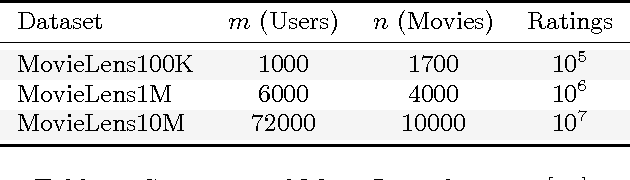
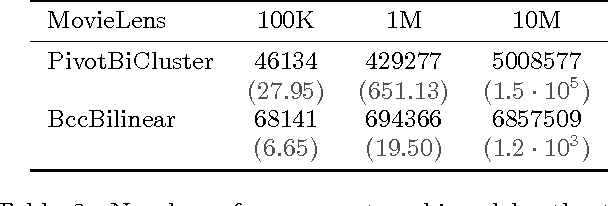
In Bipartite Correlation Clustering (BCC) we are given a complete bipartite graph $G$ with `+' and `-' edges, and we seek a vertex clustering that maximizes the number of agreements: the number of all `+' edges within clusters plus all `-' edges cut across clusters. BCC is known to be NP-hard. We present a novel approximation algorithm for $k$-BCC, a variant of BCC with an upper bound $k$ on the number of clusters. Our algorithm outputs a $k$-clustering that provably achieves a number of agreements within a multiplicative ${(1-\delta)}$-factor from the optimal, for any desired accuracy $\delta$. It relies on solving a combinatorially constrained bilinear maximization on the bi-adjacency matrix of $G$. It runs in time exponential in $k$ and $\delta^{-1}$, but linear in the size of the input. Further, we show that, in the (unconstrained) BCC setting, an ${(1-\delta)}$-approximation can be achieved by $O(\delta^{-1})$ clusters regardless of the size of the graph. In turn, our $k$-BCC algorithm implies an Efficient PTAS for the BCC objective of maximizing agreements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge