Choosing the Sample with Lowest Loss makes SGD Robust
Paper and Code
Jan 10, 2020

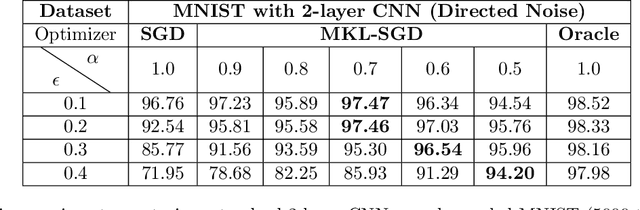
The presence of outliers can potentially significantly skew the parameters of machine learning models trained via stochastic gradient descent (SGD). In this paper we propose a simple variant of the simple SGD method: in each step, first choose a set of k samples, then from these choose the one with the smallest current loss, and do an SGD-like update with this chosen sample. Vanilla SGD corresponds to k = 1, i.e. no choice; k >= 2 represents a new algorithm that is however effectively minimizing a non-convex surrogate loss. Our main contribution is a theoretical analysis of the robustness properties of this idea for ML problems which are sums of convex losses; these are backed up with linear regression and small-scale neural network experiments
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge