Double Auctions with Two-sided Bandit Feedback
Paper and Code
Aug 13, 2022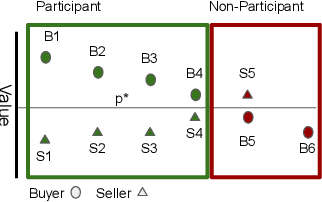
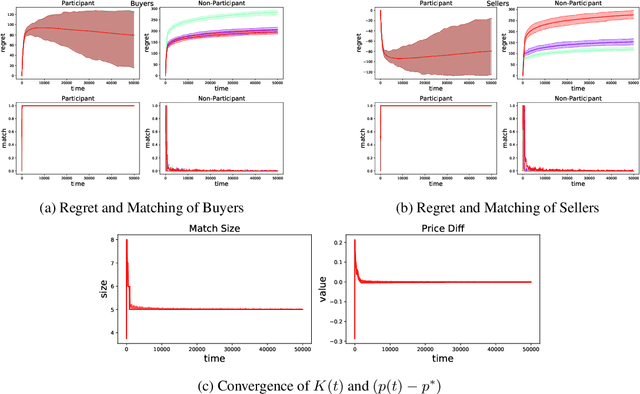
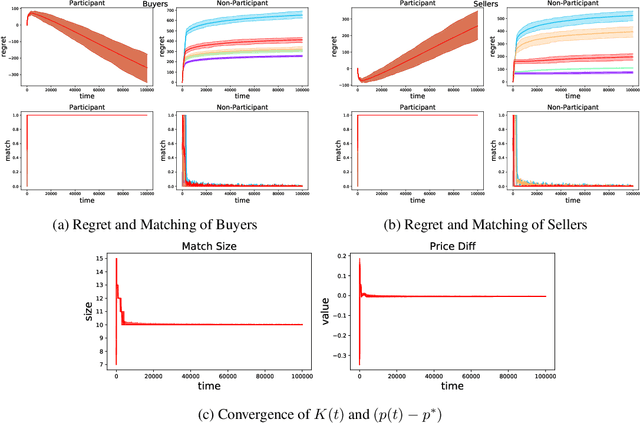
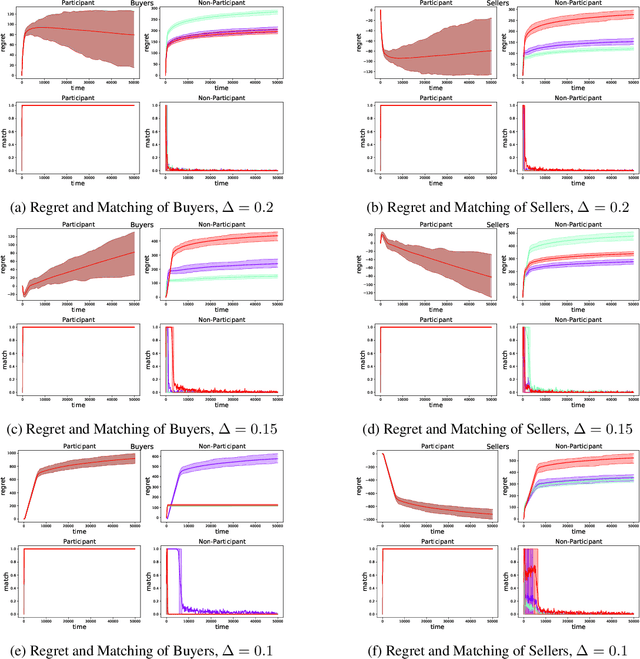
Double Auction enables decentralized transfer of goods between multiple buyers and sellers, thus underpinning functioning of many online marketplaces. Buyers and sellers compete in these markets through bidding, but do not often know their own valuation a-priori. As the allocation and pricing happens through bids, the profitability of participants, hence sustainability of such markets, depends crucially on learning respective valuations through repeated interactions. We initiate the study of Double Auction markets under bandit feedback on both buyers' and sellers' side. We show with confidence bound based bidding, and `Average Pricing' there is an efficient price discovery among the participants. In particular, the buyers and sellers exchanging goods attain $O(\sqrt{T})$ regret in $T$ rounds. The buyers and sellers who do not benefit from exchange in turn only experience $O(\log{T}/ \Delta)$ regret in $T$ rounds where $\Delta$ is the minimum price gap. We augment our upper bound by showing that even with a known fixed price of the good -- a simpler learning problem than Double Auction -- $\omega(\sqrt{T})$ regret is unattainable in certain markets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge