Competing Bandits in Decentralized Large Contextual Matching Markets

Sequential learning in a multi-agent resource constrained matching market has received significant interest in the past few years. We study decentralized learning in two-sided matching markets where the demand side (aka players or agents) competes for a `large' supply side (aka arms) with potentially time-varying preferences, to obtain a stable match. Despite a long line of work in the recent past, existing learning algorithms such as Explore-Then-Commit or Upper-Confidence-Bound remain inefficient for this problem. In particular, the per-agent regret achieved by these algorithms scales linearly with the number of arms, $K$. Motivated by the linear contextual bandit framework, we assume that for each agent an arm-mean can be represented by a linear function of a known feature vector and an unknown (agent-specific) parameter. Moreover, our setup captures the essence of a dynamic (non-stationary) matching market where the preferences over arms change over time. Our proposed algorithms achieve instance-dependent logarithmic regret, scaling independently of the number of arms, $K$.

Online Heavy-tailed Change-point detection

We study algorithms for online change-point detection (OCPD), where samples that are potentially heavy-tailed, are presented one at a time and a change in the underlying mean must be detected as early as possible. We present an algorithm based on clipped Stochastic Gradient Descent (SGD), that works even if we only assume that the second moment of the data generating process is bounded. We derive guarantees on worst-case, finite-sample false-positive rate (FPR) over the family of all distributions with bounded second moment. Thus, our method is the first OCPD algorithm that guarantees finite-sample FPR, even if the data is high dimensional and the underlying distributions are heavy-tailed. The technical contribution of our paper is to show that clipped-SGD can estimate the mean of a random vector and simultaneously provide confidence bounds at all confidence values. We combine this robust estimate with a union bound argument and construct a sequential change-point algorithm with finite-sample FPR guarantees. We show empirically that our algorithm works well in a variety of situations, whether the underlying data are heavy-tailed, light-tailed, high dimensional or discrete. No other algorithm achieves bounded FPR theoretically or empirically, over all settings we study simultaneously.

Predict-and-Critic: Accelerated End-to-End Predictive Control for Cloud Computing through Reinforcement Learning

Cloud computing holds the promise of reduced costs through economies of scale. To realize this promise, cloud computing vendors typically solve sequential resource allocation problems, where customer workloads are packed on shared hardware. Virtual machines (VM) form the foundation of modern cloud computing as they help logically abstract user compute from shared physical infrastructure. Traditionally, VM packing problems are solved by predicting demand, followed by a Model Predictive Control (MPC) optimization over a future horizon. We introduce an approximate formulation of an industrial VM packing problem as an MILP with soft-constraints parameterized by the predictions. Recently, predict-and-optimize (PnO) was proposed for end-to-end training of prediction models by back-propagating the cost of decisions through the optimization problem. But, PnO is unable to scale to the large prediction horizons prevalent in cloud computing. To tackle this issue, we propose the Predict-and-Critic (PnC) framework that outperforms PnO with just a two-step horizon by leveraging reinforcement learning. PnC jointly trains a prediction model and a terminal Q function that approximates cost-to-go over a long horizon, by back-propagating the cost of decisions through the optimization problem \emph{and from the future}. The terminal Q function allows us to solve a much smaller two-step horizon optimization problem than the multi-step horizon necessary in PnO. We evaluate PnO and the PnC framework on two datasets, three workloads, and with disturbances not modeled in the optimization problem. We find that PnC significantly improves decision quality over PnO, even when the optimization problem is not a perfect representation of reality. We also find that hardening the soft constraints of the MILP and back-propagating through the constraints improves decision quality for both PnO and PnC.

Double Auctions with Two-sided Bandit Feedback

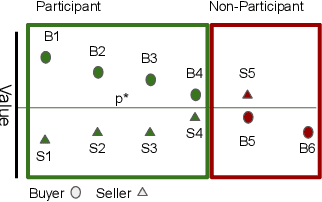
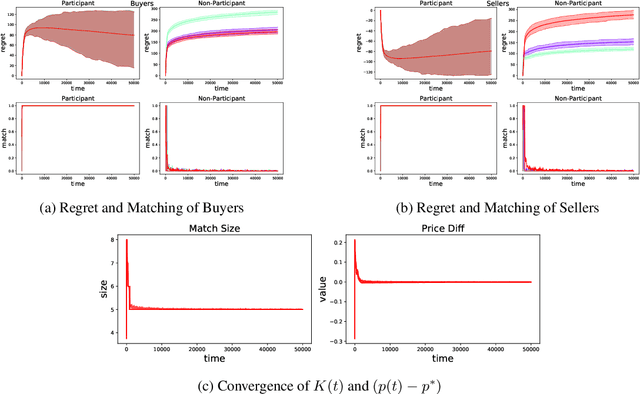
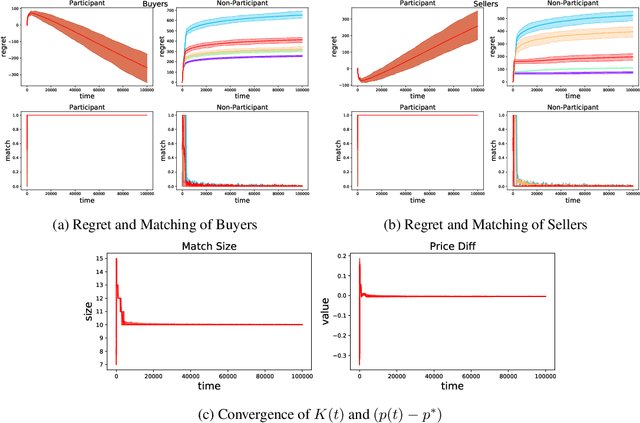
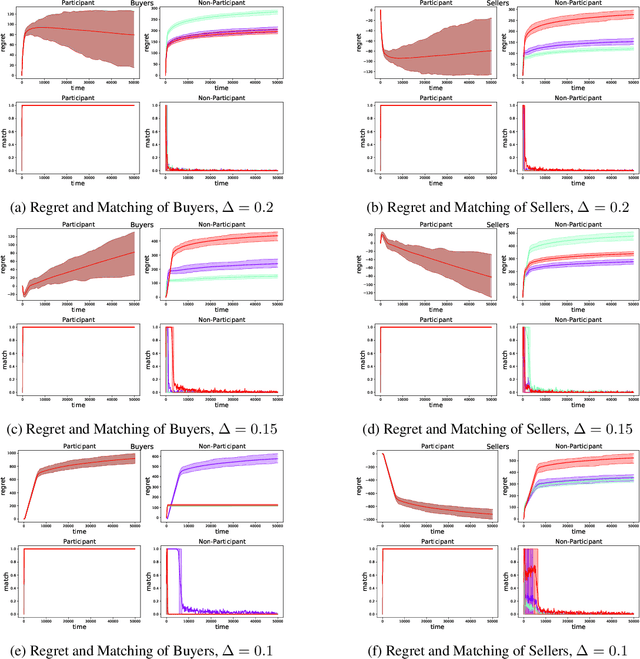
Double Auction enables decentralized transfer of goods between multiple buyers and sellers, thus underpinning functioning of many online marketplaces. Buyers and sellers compete in these markets through bidding, but do not often know their own valuation a-priori. As the allocation and pricing happens through bids, the profitability of participants, hence sustainability of such markets, depends crucially on learning respective valuations through repeated interactions. We initiate the study of Double Auction markets under bandit feedback on both buyers' and sellers' side. We show with confidence bound based bidding, and `Average Pricing' there is an efficient price discovery among the participants. In particular, the buyers and sellers exchanging goods attain $O(\sqrt{T})$ regret in $T$ rounds. The buyers and sellers who do not benefit from exchange in turn only experience $O(\log{T}/ \Delta)$ regret in $T$ rounds where $\Delta$ is the minimum price gap. We augment our upper bound by showing that even with a known fixed price of the good -- a simpler learning problem than Double Auction -- $\omega(\sqrt{T})$ regret is unattainable in certain markets.

Decentralized Competing Bandits in Non-Stationary Matching Markets

Understanding complex dynamics of two-sided online matching markets, where the demand-side agents compete to match with the supply-side (arms), has recently received substantial interest. To that end, in this paper, we introduce the framework of decentralized two-sided matching market under non stationary (dynamic) environments. We adhere to the serial dictatorship setting, where the demand-side agents have unknown and different preferences over the supply-side (arms), but the arms have fixed and known preference over the agents. We propose and analyze a decentralized and asynchronous learning algorithm, namely Decentralized Non-stationary Competing Bandits (\texttt{DNCB}), where the agents play (restrictive) successive elimination type learning algorithms to learn their preference over the arms. The complexity in understanding such a system stems from the fact that the competing bandits choose their actions in an asynchronous fashion, and the lower ranked agents only get to learn from a set of arms, not \emph{dominated} by the higher ranked agents, which leads to \emph{forced exploration}. With carefully defined complexity parameters, we characterize this \emph{forced exploration} and obtain sub-linear (logarithmic) regret of \texttt{DNCB}. Furthermore, we validate our theoretical findings via experiments.

Breaking the $\sqrt{T}$ Barrier: Instance-Independent Logarithmic Regret in Stochastic Contextual Linear Bandits

We prove an instance independent (poly) logarithmic regret for stochastic contextual bandits with linear payoff. Previously, in \cite{chu2011contextual}, a lower bound of $\mathcal{O}(\sqrt{T})$ is shown for the contextual linear bandit problem with arbitrary (adversarily chosen) contexts. In this paper, we show that stochastic contexts indeed help to reduce the regret from $\sqrt{T}$ to $\polylog(T)$. We propose Low Regret Stochastic Contextual Bandits (\texttt{LR-SCB}), which takes advantage of the stochastic contexts and performs parameter estimation (in $\ell_2$ norm) and regret minimization simultaneously. \texttt{LR-SCB} works in epochs, where the parameter estimation of the previous epoch is used to reduce the regret of the current epoch. The (poly) logarithmic regret of \texttt{LR-SCB} stems from two crucial facts: (a) the application of a norm adaptive algorithm to exploit the parameter estimation and (b) an analysis of the shifted linear contextual bandit algorithm, showing that shifting results in increasing regret. We have also shown experimentally that stochastic contexts indeed incurs a regret that scales with $\polylog(T)$.

Model Selection for Generic Contextual Bandits

We consider the problem of model selection for the general stochastic contextual bandits under the realizability assumption. We propose a successive refinement based algorithm called Adaptive Contextual Bandit ({\ttfamily ACB}), that works in phases and successively eliminates model classes that are too simple to fit the given instance. We prove that this algorithm is adaptive, i.e., the regret rate order-wise matches that of {\ttfamily FALCON}, the state-of-art contextual bandit algorithm of Levi et. al '20, that needs knowledge of the true model class. The price of not knowing the correct model class is only an additive term contributing to the second order term in the regret bound. This cost possess the intuitive property that it becomes smaller as the model class becomes easier to identify, and vice-versa. We then show that a much simpler explore-then-commit (ETC) style algorithm also obtains a regret rate of matching that of {\ttfamily FALCON}, despite not knowing the true model class. However, the cost of model selection is higher in ETC as opposed to in {\ttfamily ACB}, as expected. Furthermore, {\ttfamily ACB} applied to the linear bandit setting with unknown sparsity, order-wise recovers the model selection guarantees previously established by algorithms tailored to the linear setting.

Collaborative Learning and Personalization in Multi-Agent Stochastic Linear Bandits

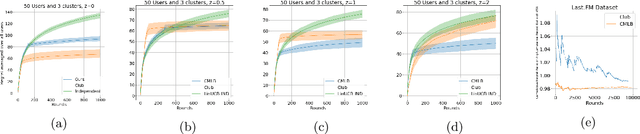
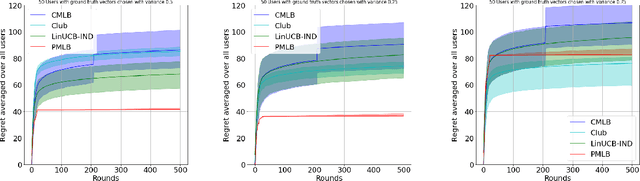
We consider the problem of minimizing regret in an $N$ agent heterogeneous stochastic linear bandits framework, where the agents (users) are similar but not all identical. We model user heterogeneity using two popularly used ideas in practice; (i) A clustering framework where users are partitioned into groups with users in the same group being identical to each other, but different across groups, and (ii) a personalization framework where no two users are necessarily identical, but a user's parameters are close to that of the population average. In the clustered users' setup, we propose a novel algorithm, based on successive refinement of cluster identities and regret minimization. We show that, for any agent, the regret scales as $\mathcal{O}(\sqrt{T/N})$, if the agent is in a `well separated' cluster, or scales as $\mathcal{O}(T^{\frac{1}{2} + \varepsilon}/(N)^{\frac{1}{2} -\varepsilon})$ if its cluster is not well separated, where $\varepsilon$ is positive and arbitrarily close to $0$. Our algorithm is adaptive to the cluster separation, and is parameter free -- it does not need to know the number of clusters, separation and cluster size, yet the regret guarantee adapts to the inherent complexity. In the personalization framework, we introduce a natural algorithm where, the personal bandit instances are initialized with the estimates of the global average model. We show that, an agent $i$ whose parameter deviates from the population average by $\epsilon_i$, attains a regret scaling of $\widetilde{O}(\epsilon_i\sqrt{T})$. This demonstrates that if the user representations are close (small $\epsilon_i)$, the resulting regret is low, and vice-versa. The results are empirically validated and we observe superior performance of our adaptive algorithms over non-adaptive baselines.

Beyond $\log^2$ Regret for Decentralized Bandits in Matching Markets

We design decentralized algorithms for regret minimization in the two-sided matching market with one-sided bandit feedback that significantly improves upon the prior works (Liu et al. 2020a, 2020b, Sankararaman et al. 2020). First, for general markets, for any $\varepsilon > 0$, we design an algorithm that achieves a $O(\log^{1+\varepsilon}(T))$ regret to the agent-optimal stable matching, with unknown time horizon $T$, improving upon the $O(\log^{2}(T))$ regret achieved in (Liu et al. 2020b). Second, we provide the optimal $\Theta(\log(T))$ agent-optimal regret for markets satisfying uniqueness consistency -- markets where leaving participants don't alter the original stable matching. Previously, $\Theta(\log(T))$ regret was achievable (Sankararaman et al. 2020, Liu et al. 2020b) in the much restricted serial dictatorship setting, when all arms have the same preference over the agents. We propose a phase-based algorithm, wherein each phase, besides deleting the globally communicated dominated arms the agents locally delete arms with which they collide often. This local deletion is pivotal in breaking deadlocks arising from rank heterogeneity of agents across arms. We further demonstrate the superiority of our algorithm over existing works through simulations.

Multi-Agent Low-Dimensional Linear Bandits

We study a multi-agent stochastic linear bandit with side information, parameterized by an unknown vector $\theta^* \in \mathbb{R}^d$. The side information consists of a finite collection of low-dimensional subspaces, one of which contains $\theta^*$. In our setting, agents can collaborate to reduce regret by sending recommendations across a communication graph connecting them. We present a novel decentralized algorithm, where agents communicate subspace indices with each other, and each agent plays a projected variant of LinUCB on the corresponding (low-dimensional) subspace. Through a combination of collaborative best subspace identification, and per-agent learning of an unknown vector in the corresponding low-dimensional subspace, we show that the per-agent regret is much smaller than the case when agents do not communicate. By collaborating to identify the subspace containing $\theta^*$, we show that each agent effectively solves an easier instance of the linear bandit (compared to the case of no collaboration), thus leading to the reduced per-agent regret. We finally complement these results through simulations.