Contextual Blocking Bandits

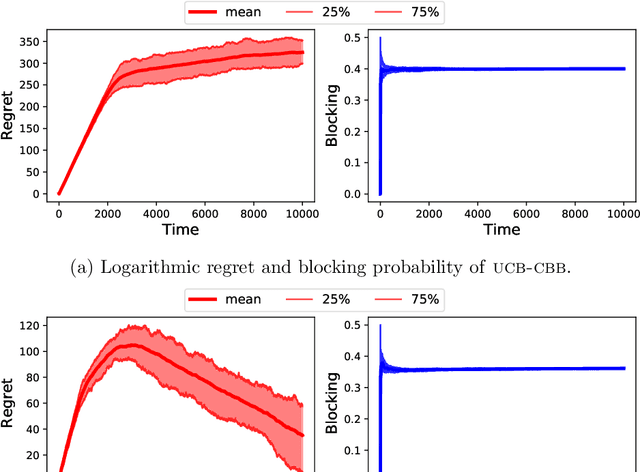
We study a novel variant of the multi-armed bandit problem, where at each time step, the player observes a context that determines the arms' mean rewards. However, playing an arm blocks it (across all contexts) for a fixed number of future time steps. This model extends the blocking bandits model (Basu et al., NeurIPS19) to a contextual setting, and captures important scenarios such as recommendation systems or ad placement with diverse users, and processing diverse pool of jobs. This contextual setting, however, invalidates greedy solution techniques that are effective for its non-contextual counterpart. Assuming knowledge of the mean reward for each arm-context pair, we design a randomized LP-based algorithm which is $\alpha$-optimal in (large enough) $T$ time steps, where $\alpha = \tfrac{d_{\max}}{2d_{\max}-1}\left(1- \epsilon\right)$ for any $\epsilon >0$, and $d_{max}$ is the maximum delay of the arms. In the bandit setting, we show that a UCB based variant of the above online policy guarantees $\mathcal{O}\left(\log T\right)$ regret w.r.t. the $\alpha$-optimal strategy in $T$ time steps, which matches the $\Omega(\log(T))$ regret lower bound in this setting. Due to the time correlation caused by the blocking of arms, existing techniques for upper bounding regret fail. As a first, in the presence of such temporal correlations, we combine ideas from coupling of non-stationary Markov chains and opportunistic sub-sampling with suboptimality charging techniques from combinatorial bandits to prove our regret upper bounds.