The Countable-armed Bandit with Vanishing Arms

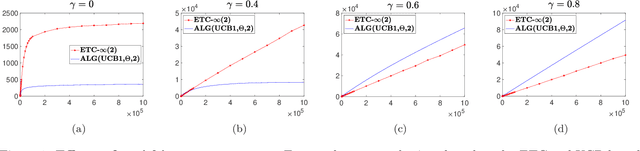
We consider a bandit problem with countably many arms, partitioned into finitely many "types," each characterized by a unique mean reward. A "non-stationary" distribution governs the relative abundance of each arm-type in the population of arms, aka the "arm-reservoir." This non-stationarity is attributable to a probabilistic leakage of "optimal" arms from the reservoir over time, which we refer to as the "vanishing arms" phenomenon; this induces a time-varying (potentially "endogenous," policy-dependent) distribution over the reservoir. The objective is minimization of the expected cumulative regret. We characterize necessary and sufficient conditions for achievability of sub-linear regret in terms of a critical vanishing rate of optimal arms. We also discuss two reservoir distribution-oblivious algorithms that are long-run-average optimal whenever sub-linear regret is statistically achievable. Numerical experiments highlight a distinctive characteristic of this problem related to ex ante knowledge of the "gap" parameter (the difference between the top two mean rewards): in contrast to the stationary bandit formulation, regret in our setting may suffer substantial inflation under adaptive exploration-based (gap-oblivious) algorithms such as UCB vis-`a-vis their non-adaptive forced exploration-based (gap-aware) counterparts like ETC.