Doubly-Robust Lasso Bandit

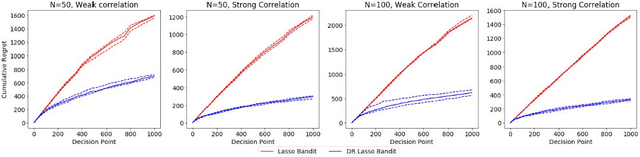
Contextual multi-armed bandit algorithms are widely used in sequential decision tasks such as news article recommendation systems, web page ad placement algorithms, and mobile health. Most of the existing algorithms have regret proportional to a polynomial function of the context dimension, $d$. In many applications however, it is often the case that contexts are high-dimensional with only a sparse subset of size $s_0 (\ll d)$ being correlated with the reward. We propose a novel algorithm, namely the Doubly-Robust Lasso Bandit algorithm, which exploits the sparse structure as in Lasso, while blending the doubly-robust technique used in missing data literature. The high-probability upper bound of the regret incurred by the proposed algorithm does not depend on the number of arms, has better dependency on $s_0$ than previous works, and scales with $\mathrm{log}(d)$ instead of a polynomial function of $d$. The proposed algorithm shows good performance when contexts of different arms are correlated and requires less tuning parameters than existing methods.