Learning Massive-scale Partial Correlation Networks in Clinical Multi-omics Studies with HP-ACCORD

Graphical model estimation from modern multi-omics data requires a balance between statistical estimation performance and computational scalability. We introduce a novel pseudolikelihood-based graphical model framework that reparameterizes the target precision matrix while preserving sparsity pattern and estimates it by minimizing an $\ell_1$-penalized empirical risk based on a new loss function. The proposed estimator maintains estimation and selection consistency in various metrics under high-dimensional assumptions. The associated optimization problem allows for a provably fast computation algorithm using a novel operator-splitting approach and communication-avoiding distributed matrix multiplication. A high-performance computing implementation of our framework was tested in simulated data with up to one million variables demonstrating complex dependency structures akin to biological networks. Leveraging this scalability, we estimated partial correlation network from a dual-omic liver cancer data set. The co-expression network estimated from the ultrahigh-dimensional data showed superior specificity in prioritizing key transcription factors and co-activators by excluding the impact of epigenomic regulation, demonstrating the value of computational scalability in multi-omic data analysis. %derived from the gene expression data.

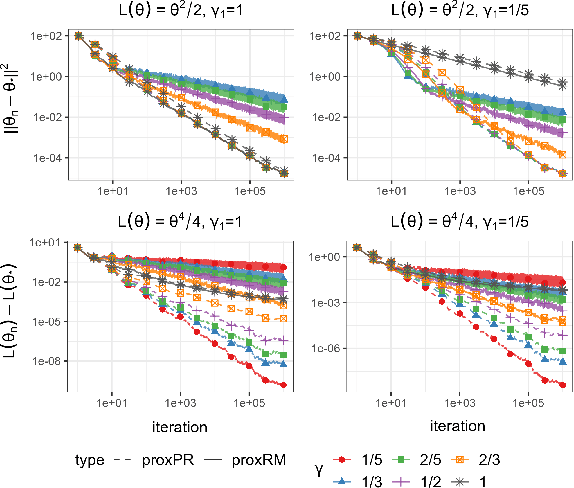
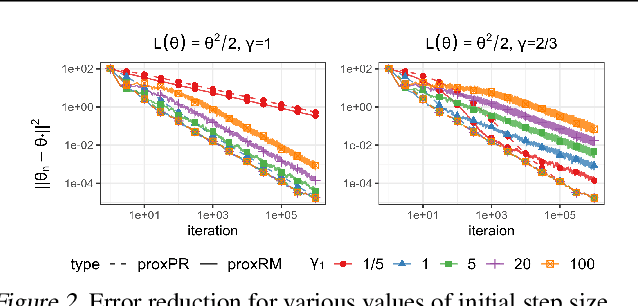
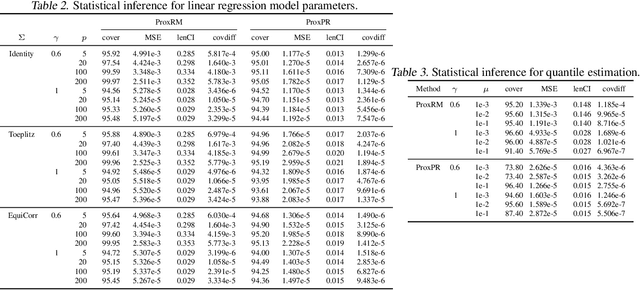
Statistical inference with implicit SGD: proximal Robbins-Monro vs. Polyak-Ruppert

The implicit stochastic gradient descent (ISGD), a proximal version of SGD, is gaining interest in the literature due to its stability over (explicit) SGD. In this paper, we conduct an in-depth analysis of the two modes of ISGD for smooth convex functions, namely proximal Robbins-Monro (proxRM) and proximal Poylak-Ruppert (proxPR) procedures, for their use in statistical inference on model parameters. Specifically, we derive non-asymptotic point estimation error bounds of both proxRM and proxPR iterates and their limiting distributions, and propose on-line estimators of their asymptotic covariance matrices that require only a single run of ISGD. The latter estimators are used to construct valid confidence intervals for the model parameters. Our analysis is free of the generalized linear model assumption that has limited the preceding analyses, and employs feasible procedures. Our on-line covariance matrix estimators appear to be the first of this kind in the ISGD literature.