Seg2Grasp: A Robust Modular Suction Grasping in Bin Picking

Current bin picking methods that rely heavily on end-to-end learning often falter when confronted with unfamiliar or complex objects in unstructured environments. To overcome these limitations, we introduce Seg2Grasp, a modular pipeline designed for robust suction grasping in dynamic and cluttered bin scenarios. Seg2Grasp is built on a three-step process: Segmentation, Grasping, and Classification. The Segmentation module employs a Transformer-based model to generate class-agnostic object masks from RGB-D images, ensuring accurate detection across various conditions. The Grasping module uses surface normals and mask proposals to determine the optimal suction points, enhancing grasp success. Finally, the Classification module leverages fine-tuned open-vocabulary Mask-CLIP for precise object identification, enabling versatile handling of diverse objects. Real-world robotic experiments demonstrate that Seg2Grasp outperforms existing methods in success rates and adaptability, establishing it as a powerful tool for automated bin picking in industrial settings.

DA-Fusion: Deformable Attention-Based RGB-D Fusion Transformer for Unseen Object Instance Segmentation

In logistics automation, precise segmentation of unseen objects is crucial for efficient robotic manipulation in cluttered environments. Tasks such as bin-picking and shelf-picking require robust perception to handle occlusions, varying object shapes, and complex spatial arrangements. Traditional RGB-based methods tend to over-segment objects due to their reliance on texture, while depth-based methods often under-segment by focusing primarily on geometric features. To address these limitations, we propose DA-Fusion, a deformable attention-based RGB-D fusion Transformer designed for unseen object instance segmentation. DA-Fusion effectively combines the strengths of both RGB and depth data, enhancing segmentation accuracy in cluttered and multi-layered object environments. We also introduce the Object Clutter Bin Dataset (OCBD), a benchmark dataset specifically tailored for evaluating bin-picking scenarios in top-down views. Extensive evaluations demonstrate that DA-Fusion outperforms state-of-the-art methods across diverse environments, making it particularly suited for real-world logistics tasks.

CDIS: Cross-Dimensional Class-Agnostic 3D Instance Segmentation via 2D Mask Tracking and 3D-2D Projection Merging

Class-agnostic 3D instance segmentation is critical for robotic systems operating in unknown environments, enabling perception of previously unseen objects for reliable manipulation and navigation. Existing approaches typically project per-frame 2D instance masks into 3D and merge them, which often breaks object identities across time and yields fragmented 3D instances. We introduce Cross-Dimensional Class-Agnostic 3D Instance Segmentation (CDIS), a zero-shot framework that explicitly tracks 2D instance masks across frames and associates them with 3D superpoints, creating a feedback loop between 2D and 3D. This cross-dimensional reasoning links temporally stable 2D tracks with spatially coherent 3D regions, producing globally consistent 3D instance labels without any 3D-specific training. Experiments on benchmark datasets demonstrate that CDIS achieves higher accuracy and consistency than state-of-the-art zero-shot methods, while remaining efficient and scalable to diverse real-world environments.

When Does Online Imitation Learning Help in LLM Post-Training? The Role of (Non-)Realizability Beyond Horizon

Online imitation learning (IL), particularly on-policy distillation, has emerged as a strong LLM post-training approach, often outperforming offline supervised fine-tuning (SFT). Yet a principled understanding of when and why online interaction helps remains unclear. In this work, we challenge the view that error accumulation is the main source of online IL's advantage, and instead show that the benefits of online interaction depend critically on whether the setting is realizable, i.e., whether the student policy class can represent the expert policy. Under realizability, we empirically find that offline IL already matches expert performance. In contrast, in non-realizable (misspecified) settings, we prove that offline IL encounters an information-theoretic bottleneck even when horizon $H=1$, and propose a structural characterization of misspecification relative to the reward, under which online IL provably achieves high performance despite a large distributional mismatch between the expert and student policies.

Provable Benefits of RLVR over SFT for Reasoning Models: Learning to Backtrack Efficiently

Recent advances in large language models (LLMs) have demonstrated that reinforcement fine-tuning of pretrained base models can lead to significant gains in reasoning performance at inference time. In this work, we theoretically analyze why reinforcement fine-tuning induces better reasoning ability than purely supervised fine-tuning (SFT) methods. We model chain-of-thought (CoT) reasoning as a pathfinding problem on graphs and compare the popular method of reinforcement learning with verifiable rewards (RLVR) against traditional SFT. We prove that SFT, when trained on golden shortest paths without negative examples, fails to learn how to efficiently backtrack. In contrast, an RLVR-trained model can learn how to efficiently backtrack from dead ends using only outcome reward. This leads to an exponential separation in inference-time compute between the two methods, and demonstrates that RLVR leads the model to learn the location of difficult decisions in a reasoning chain, ultimately allowing for better allocation of inference-time compute. Finally, we show that the reasoning traces of an RLVR model can be distilled to train a base model to backtrack efficiently as well.

Sharp Capacity Thresholds in Linear Associative Memory: From Winner-Take-All to Listwise Retrieval

How many key-value associations can a $d\times d$ linear memory store? We show that the answer depends not only on the $d^2$ degrees of freedom in the memory matrix, but also on the retrieval criterion. In an isotropic Gaussian model for the stored pairs, we show that top-1 retrieval, where every signal must beat its largest distractor, requires the logarithmic model-size scale $d^2\asymp n\log n$. We prove that the correlation matrix memory construction, which stores associations by superposing key-target outer products, achieves this scale through a sharp phase transition, and that the same scaling is necessary for any linear memory. Thus the logarithm is the intrinsic extreme-value price of winner-take-all decoding. We next consider listwise retrieval, where the correct target need not be the unique top-scoring item but should remain among the strongest candidates. To formalize this regime, we propose the Tail-Average Margin (TAM), a convex upper-tail criterion that certifies inclusion of the correct target in a controlled candidate list. Under this listwise retrieval criterion, the capacity follows the quadratic scale $d^2\asymp n$. At load $n/d^2\toα$, we develop an exact asymptotic theory for the TAM empirical-risk minimizer through a two-parameter scalar variational principle. The theory has a rich phenomenology: in the ridgeless limit it yields a closed-form critical load separating satisfiable and unsatisfiable phases, and it predicts the limiting laws of true scores, competitor scores, margins, and percentile profiles. Finally, a small-tail extrapolation further leads to the conjectural sharp top-1 threshold $d^2\sim 2n\log n$.

Sharp Capacity Scaling of Spectral Optimizers in Learning Associative Memory

Spectral optimizers such as Muon have recently shown strong empirical performance in large-scale language model training, but the source and extent of their advantage remain poorly understood. We study this question through the linear associative memory problem, a tractable model for factual recall in transformer-based models. In particular, we go beyond orthogonal embeddings and consider Gaussian inputs and outputs, which allows the number of stored associations to greatly exceed the embedding dimension. Our main result sharply characterizes the recovery rates of one step of Muon and SGD on the logistic regression loss under a power law frequency distribution. We show that the storage capacity of Muon significantly exceeds that of SGD, and moreover Muon saturates at a larger critical batch size. We further analyze the multi-step dynamics under a thresholded gradient approximation and show that Muon achieves a substantially faster initial recovery rate than SGD, while both methods eventually converge to the information-theoretic limit at comparable speeds. Experiments on synthetic tasks validate the predicted scaling laws. Our analysis provides a quantitative understanding of the signal amplification of Muon and lays the groundwork for establishing scaling laws across more practical language modeling tasks and optimizers.

Coverage Improvement and Fast Convergence of On-policy Preference Learning

Online on-policy preference learning algorithms for language model alignment such as online direct policy optimization (DPO) can significantly outperform their offline counterparts. We provide a theoretical explanation for this phenomenon by analyzing how the sampling policy's coverage evolves throughout on-policy training. We propose and rigorously justify the \emph{coverage improvement principle}: with sufficient batch size, each update moves into a region around the target where coverage is uniformly better, making subsequent data increasingly informative and enabling rapid convergence. In the contextual bandit setting with Bradley-Terry preferences and linear softmax policy class, we show that on-policy DPO converges exponentially in the number of iterations for batch size exceeding a generalized coverage threshold. In contrast, any learner restricted to offline samples from the initial policy suffers a slower minimax rate, leading to a sharp separation in total sample complexity. Motivated by this analysis, we further propose a simple hybrid sampler based on a novel \emph{preferential} G-optimal design, which removes dependence on coverage and guarantees convergence in just two rounds. Finally, we develop principled on-policy schemes for reward distillation in the general function class setting, and show faster noiseless rates under an alternative deviation-based notion of coverage. Experimentally, we confirm that on-policy DPO and our proposed reward distillation algorithms outperform their off-policy counterparts and enjoy stable, monotonic performance gains across iterations.

OV-MAP : Open-Vocabulary Zero-Shot 3D Instance Segmentation Map for Robots

We introduce OV-MAP, a novel approach to open-world 3D mapping for mobile robots by integrating open-features into 3D maps to enhance object recognition capabilities. A significant challenge arises when overlapping features from adjacent voxels reduce instance-level precision, as features spill over voxel boundaries, blending neighboring regions together. Our method overcomes this by employing a class-agnostic segmentation model to project 2D masks into 3D space, combined with a supplemented depth image created by merging raw and synthetic depth from point clouds. This approach, along with a 3D mask voting mechanism, enables accurate zero-shot 3D instance segmentation without relying on 3D supervised segmentation models. We assess the effectiveness of our method through comprehensive experiments on public datasets such as ScanNet200 and Replica, demonstrating superior zero-shot performance, robustness, and adaptability across diverse environments. Additionally, we conducted real-world experiments to demonstrate our method's adaptability and robustness when applied to diverse real-world environments.

Mirror Mean-Field Langevin Dynamics

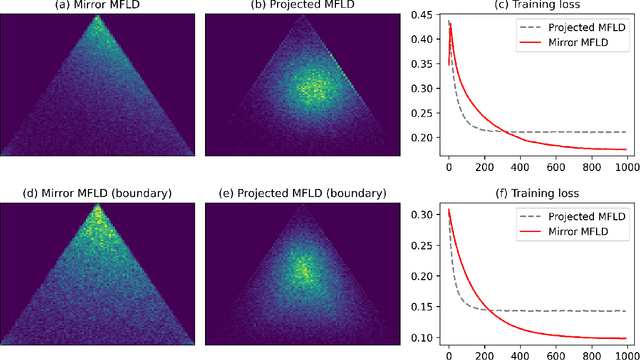
The mean-field Langevin dynamics (MFLD) minimizes an entropy-regularized nonlinear convex functional on the Wasserstein space over $\mathbb{R}^d$, and has gained attention recently as a model for the gradient descent dynamics of interacting particle systems such as infinite-width two-layer neural networks. However, many problems of interest have constrained domains, which are not solved by existing mean-field algorithms due to the global diffusion term. We study the optimization of probability measures constrained to a convex subset of $\mathbb{R}^d$ by proposing the \emph{mirror mean-field Langevin dynamics} (MMFLD), an extension of MFLD to the mirror Langevin framework. We obtain linear convergence guarantees for the continuous MMFLD via a uniform log-Sobolev inequality, and uniform-in-time propagation of chaos results for its time- and particle-discretized counterpart.