SAMIRO: Spatial Attention Mutual Information Regularization with a Pre-trained Model as Oracle for Lane Detection

Lane detection is an important topic in the future mobility solutions. Real-world environmental challenges such as background clutter, varying illumination, and occlusions pose significant obstacles to effective lane detection, particularly when relying on data-driven approaches that require substantial effort and cost for data collection and annotation. To address these issues, lane detection methods must leverage contextual and global information from surrounding lanes and objects. In this paper, we propose a Spatial Attention Mutual Information Regularization with a pre-trained model as an Oracle, called SAMIRO. SAMIRO enhances lane detection performance by transferring knowledge from a pretrained model while preserving domain-agnostic spatial information. Leveraging SAMIRO's plug-and-play characteristic, we integrate it into various state-of-the-art lane detection approaches and conduct extensive experiments on major benchmarks such as CULane, Tusimple, and LLAMAS. The results demonstrate that SAMIRO consistently improves performance across different models and datasets. The code will be made available upon publication.

$t^3$-Variational Autoencoder: Learning Heavy-tailed Data with Student's t and Power Divergence

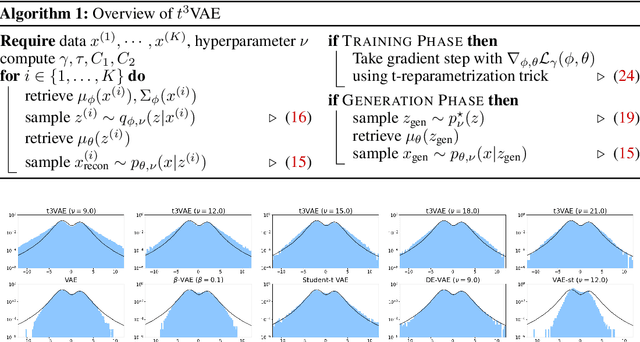
The variational autoencoder (VAE) typically employs a standard normal prior as a regularizer for the probabilistic latent encoder. However, the Gaussian tail often decays too quickly to effectively accommodate the encoded points, failing to preserve crucial structures hidden in the data. In this paper, we explore the use of heavy-tailed models to combat over-regularization. Drawing upon insights from information geometry, we propose $t^3$VAE, a modified VAE framework that incorporates Student's t-distributions for the prior, encoder, and decoder. This results in a joint model distribution of a power form which we argue can better fit real-world datasets. We derive a new objective by reformulating the evidence lower bound as joint optimization of KL divergence between two statistical manifolds and replacing with $\gamma$-power divergence, a natural alternative for power families. $t^3$VAE demonstrates superior generation of low-density regions when trained on heavy-tailed synthetic data. Furthermore, we show that $t^3$VAE significantly outperforms other models on CelebA and imbalanced CIFAR-100 datasets.