The data augmentation algorithm

The data augmentation (DA) algorithms are popular Markov chain Monte Carlo (MCMC) algorithms often used for sampling from intractable probability distributions. This review article comprehensively surveys DA MCMC algorithms, highlighting their theoretical foundations, methodological implementations, and diverse applications in frequentist and Bayesian statistics. The article discusses tools for studying the convergence properties of DA algorithms. Furthermore, it contains various strategies for accelerating the speed of convergence of the DA algorithms, different extensions of DA algorithms and outlines promising directions for future research. This paper aims to serve as a resource for researchers and practitioners seeking to leverage data augmentation techniques in MCMC algorithms by providing key insights and synthesizing recent developments.

Geometric Ergodicity in Modified Variations of Riemannian Manifold and Lagrangian Monte Carlo

Riemannian manifold Hamiltonian (RMHMC) and Lagrangian Monte Carlo (LMC) have emerged as powerful methods of Bayesian inference. Unlike Euclidean Hamiltonian Monte Carlo (EHMC) and the Metropolis-adjusted Langevin algorithm (MALA), the geometric ergodicity of these Riemannian algorithms has not been extensively studied. On the other hand, the manifold Metropolis-adjusted Langevin algorithm (MMALA) has recently been shown to exhibit geometric ergodicity under certain conditions. This work investigates the mixture of the LMC and RMHMC transition kernels with MMALA in order to equip the resulting method with an "inherited" geometric ergodicity theory. We motivate this mixture kernel based on an analogy between single-step HMC and MALA. We then proceed to evaluate the original and modified transition kernels on several benchmark Bayesian inference tasks.

Analyzing Relevance Vector Machines using a single penalty approach

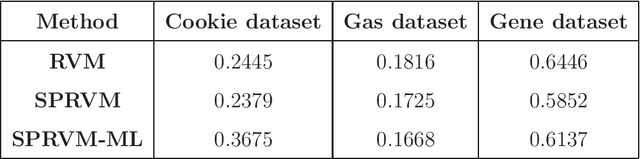
Relevance vector machine (RVM) is a popular sparse Bayesian learning model typically used for prediction. Recently it has been shown that improper priors assumed on multiple penalty parameters in RVM may lead to an improper posterior. Currently in the literature, the sufficient conditions for posterior propriety of RVM do not allow improper priors over the multiple penalty parameters. In this article, we propose a single penalty relevance vector machine (SPRVM) model in which multiple penalty parameters are replaced by a single penalty and we consider a semi Bayesian approach for fitting the SPRVM. The necessary and sufficient conditions for posterior propriety of SPRVM are more liberal than those of RVM and allow for several improper priors over the penalty parameter. Additionally, we also prove the geometric ergodicity of the Gibbs sampler used to analyze the SPRVM model and hence can estimate the asymptotic standard errors associated with the Monte Carlo estimate of the means of the posterior predictive distribution. Such a Monte Carlo standard error cannot be computed in the case of RVM, since the rate of convergence of the Gibbs sampler used to analyze RVM is not known. The predictive performance of RVM and SPRVM is compared by analyzing three real life datasets.