Analyzing Relevance Vector Machines using a single penalty approach
Paper and Code
Jul 05, 2021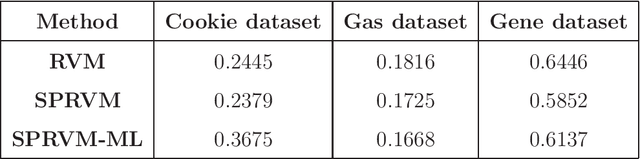
Relevance vector machine (RVM) is a popular sparse Bayesian learning model typically used for prediction. Recently it has been shown that improper priors assumed on multiple penalty parameters in RVM may lead to an improper posterior. Currently in the literature, the sufficient conditions for posterior propriety of RVM do not allow improper priors over the multiple penalty parameters. In this article, we propose a single penalty relevance vector machine (SPRVM) model in which multiple penalty parameters are replaced by a single penalty and we consider a semi Bayesian approach for fitting the SPRVM. The necessary and sufficient conditions for posterior propriety of SPRVM are more liberal than those of RVM and allow for several improper priors over the penalty parameter. Additionally, we also prove the geometric ergodicity of the Gibbs sampler used to analyze the SPRVM model and hence can estimate the asymptotic standard errors associated with the Monte Carlo estimate of the means of the posterior predictive distribution. Such a Monte Carlo standard error cannot be computed in the case of RVM, since the rate of convergence of the Gibbs sampler used to analyze RVM is not known. The predictive performance of RVM and SPRVM is compared by analyzing three real life datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge