On Manifold Learning in Plato's Cave: Remarks on Manifold Learning and Physical Phenomena

Many techniques in machine learning attempt explicitly or implicitly to infer a low-dimensional manifold structure of an underlying physical phenomenon from measurements without an explicit model of the phenomenon or the measurement apparatus. This paper presents a cautionary tale regarding the discrepancy between the geometry of measurements and the geometry of the underlying phenomenon in a benign setting. The deformation in the metric illustrated in this paper is mathematically straightforward and unavoidable in the general case, and it is only one of several similar effects. While this is not always problematic, we provide an example of an arguably standard and harmless data processing procedure where this effect leads to an incorrect answer to a seemingly simple question. Although we focus on manifold learning, these issues apply broadly to dimensionality reduction and unsupervised learning.

Using VAEs to Learn Latent Variables: Observations on Applications in cryo-EM

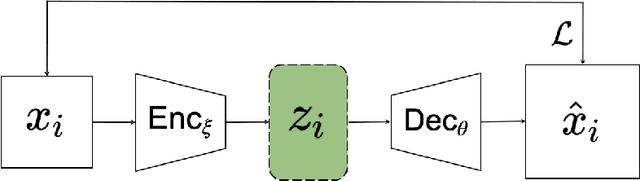
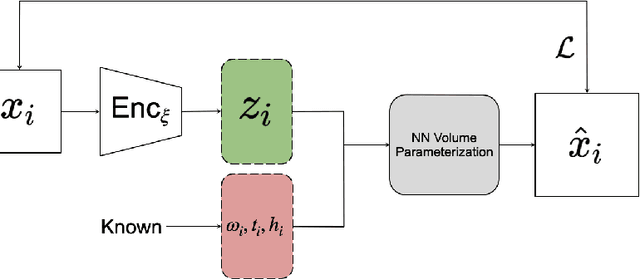
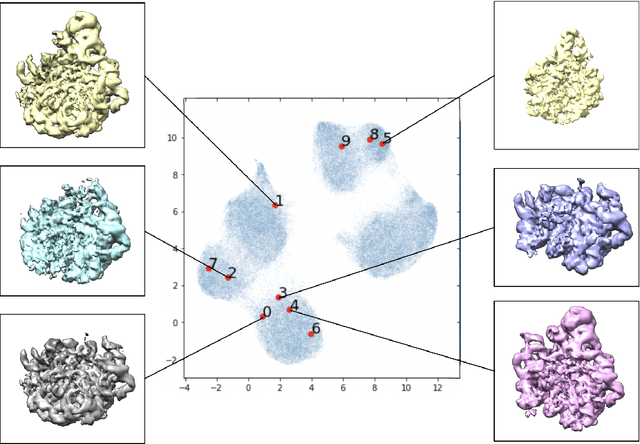
Variational autoencoders (VAEs) are a popular generative model used to approximate distributions. The encoder part of the VAE is used in amortized learning of latent variables, producing a latent representation for data samples. Recently, VAEs have been used to characterize physical and biological systems. In this case study, we qualitatively examine the amortization properties of a VAE used in biological applications. We find that in this application the encoder bears a qualitative resemblance to more traditional explicit representation of latent variables.

Geometric Ergodicity in Modified Variations of Riemannian Manifold and Lagrangian Monte Carlo

Riemannian manifold Hamiltonian (RMHMC) and Lagrangian Monte Carlo (LMC) have emerged as powerful methods of Bayesian inference. Unlike Euclidean Hamiltonian Monte Carlo (EHMC) and the Metropolis-adjusted Langevin algorithm (MALA), the geometric ergodicity of these Riemannian algorithms has not been extensively studied. On the other hand, the manifold Metropolis-adjusted Langevin algorithm (MMALA) has recently been shown to exhibit geometric ergodicity under certain conditions. This work investigates the mixture of the LMC and RMHMC transition kernels with MMALA in order to equip the resulting method with an "inherited" geometric ergodicity theory. We motivate this mixture kernel based on an analogy between single-step HMC and MALA. We then proceed to evaluate the original and modified transition kernels on several benchmark Bayesian inference tasks.

Manifold Density Estimation via Generalized Dequantization

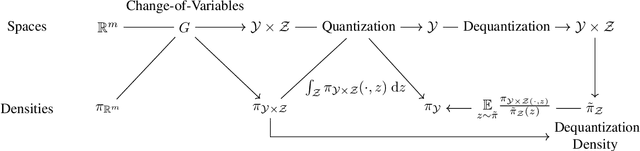
Density estimation is an important technique for characterizing distributions given observations. Much existing research on density estimation has focused on cases wherein the data lies in a Euclidean space. However, some kinds of data are not well-modeled by supposing that their underlying geometry is Euclidean. Instead, it can be useful to model such data as lying on a {\it manifold} with some known structure. For instance, some kinds of data may be known to lie on the surface of a sphere. We study the problem of estimating densities on manifolds. We propose a method, inspired by the literature on "dequantization," which we interpret through the lens of a coordinate transformation of an ambient Euclidean space and a smooth manifold of interest. Using methods from normalizing flows, we apply this method to the dequantization of smooth manifold structures in order to model densities on the sphere, tori, and the orthogonal group.

Magnetic Manifold Hamiltonian Monte Carlo

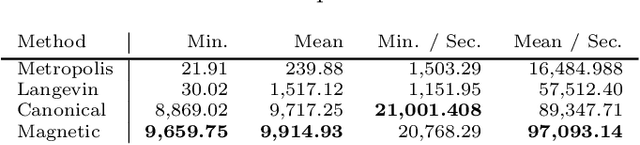
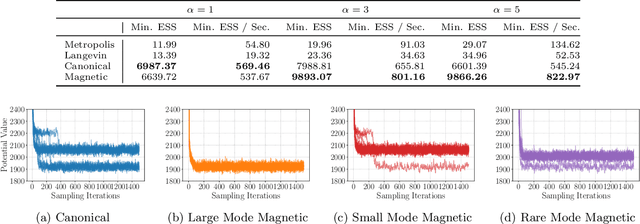
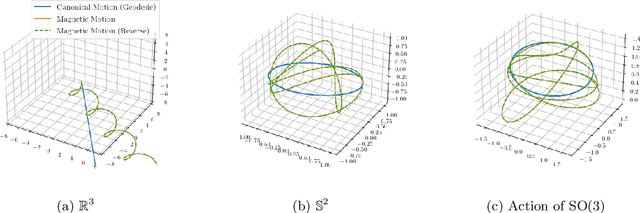
Markov chain Monte Carlo (MCMC) algorithms offer various strategies for sampling; the Hamiltonian Monte Carlo (HMC) family of samplers are MCMC algorithms which often exhibit improved mixing properties. The recently introduced magnetic HMC, a generalization of HMC motivated by the physics of particles influenced by magnetic field forces, has been demonstrated to improve the performance of HMC. In many applications, one wishes to sample from a distribution restricted to a constrained set, often manifested as an embedded manifold (for example, the surface of a sphere). We introduce magnetic manifold HMC, an HMC algorithm on embedded manifolds motivated by the physics of particles constrained to a manifold and moving under magnetic field forces. We discuss the theoretical properties of magnetic Hamiltonian dynamics on manifolds, and introduce a reversible and symplectic integrator for the HMC updates. We demonstrate that magnetic manifold HMC produces favorable sampling behaviors relative to the canonical variant of manifold-constrained HMC.

Spectral Flow on the Manifold of SPD Matrices for Multimodal Data Processing

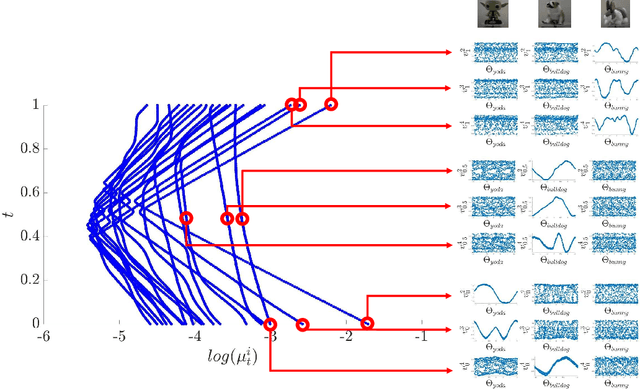
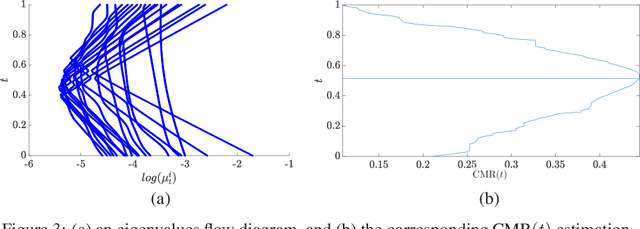
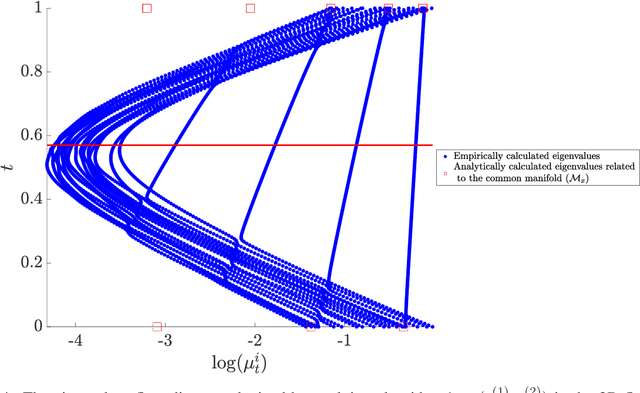
In this paper, we consider data acquired by multimodal sensors capturing complementary aspects and features of a measured phenomenon. We focus on a scenario in which the measurements share mutual sources of variability but might also be contaminated by other measurement-specific sources such as interferences or noise. Our approach combines manifold learning, which is a class of nonlinear data-driven dimension reduction methods, with the well-known Riemannian geometry of symmetric and positive-definite (SPD) matrices. Manifold learning typically includes the spectral analysis of a kernel built from the measurements. Here, we take a different approach, utilizing the Riemannian geometry of the kernels. In particular, we study the way the spectrum of the kernels changes along geodesic paths on the manifold of SPD matrices. We show that this change enables us, in a purely unsupervised manner, to derive a compact, yet informative, description of the relations between the measurements, in terms of their underlying components. Based on this result, we present new algorithms for extracting the common latent components and for identifying common and measurement-specific components.

Non-Canonical Hamiltonian Monte Carlo

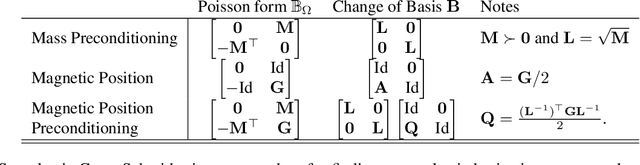
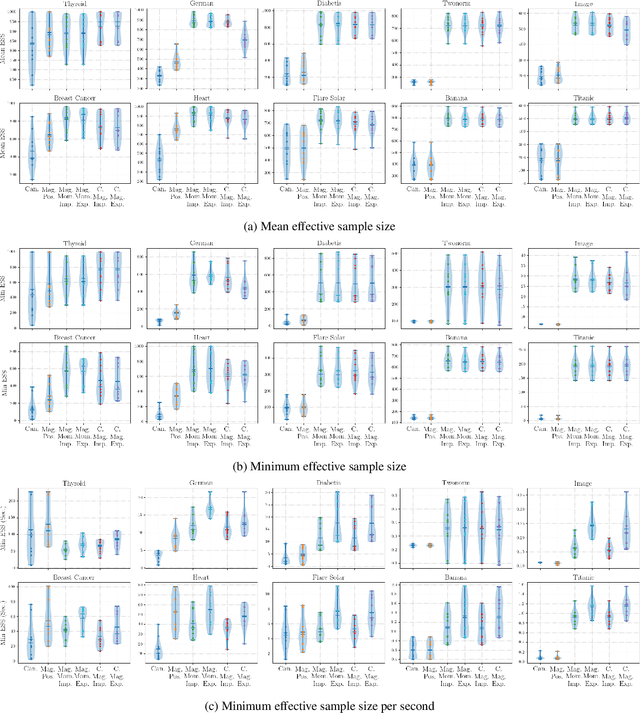
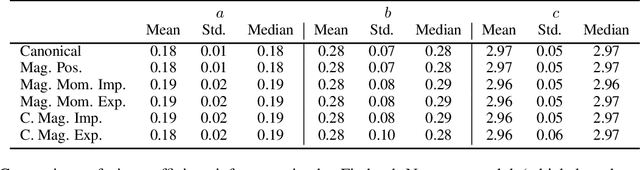
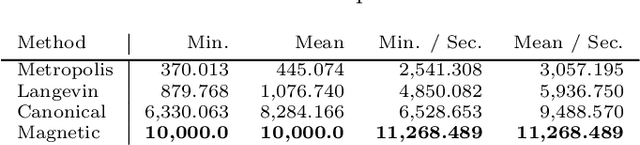
Hamiltonian Monte Carlo is typically based on the assumption of an underlying canonical symplectic structure. Numerical integrators designed for the canonical structure are incompatible with motion generated by non-canonical dynamics. These non-canonical dynamics, motivated by examples in physics and symplectic geometry, correspond to techniques such as preconditioning which are routinely used to improve algorithmic performance. Indeed, recently, a special case of non-canonical structure, magnetic Hamiltonian Monte Carlo, was demonstrated to provide advantageous sampling properties. We present a framework for Hamiltonian Monte Carlo using non-canonical symplectic structures. Our experimental results demonstrate sampling advantages associated to Hamiltonian Monte Carlo with non-canonical structure. To summarize our contributions: (i) we develop non-canonical HMC from foundations in symplectic geomtry; (ii) we construct an HMC procedure using implicit integration that satisfies the detailed balance; (iii) we propose to accelerate the sampling using an {\em approximate} explicit methodology; (iv) we study two novel, randomly-generated non-canonical structures: magnetic momentum and the coupled magnet structure, with implicit and explicit integration.

Hyper-Molecules: on the Representation and Recovery of Dynamical Structures, with Application to Flexible Macro-Molecular Structures in Cryo-EM

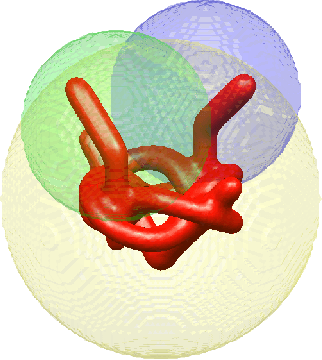
Cryo-electron microscopy (cryo-EM), the subject of the 2017 Nobel Prize in Chemistry, is a technology for determining the 3-D structure of macromolecules from many noisy 2-D projections of instances of these macromolecules, whose orientations and positions are unknown. The molecular structures are not rigid objects, but flexible objects involved in dynamical processes. The different conformations are exhibited by different instances of the macromolecule observed in a cryo-EM experiment, each of which is recorded as a particle image. The range of conformations and the conformation of each particle are not known a priori; one of the great promises of cryo-EM is to map this conformation space. Remarkable progress has been made in determining rigid structures from homogeneous samples of molecules in spite of the unknown orientation of each particle image and significant progress has been made in recovering a few distinct states from mixtures of rather distinct conformations, but more complex heterogeneous samples remain a major challenge. We introduce the ``hyper-molecule'' framework for modeling structures across different states of heterogeneous molecules, including continuums of states. The key idea behind this framework is representing heterogeneous macromolecules as high-dimensional objects, with the additional dimensions representing the conformation space. This idea is then refined to model properties such as localized heterogeneity. In addition, we introduce an algorithmic framework for recovering such maps of heterogeneous objects from experimental data using a Bayesian formulation of the problem and Markov chain Monte Carlo (MCMC) algorithms to address the computational challenges in recovering these high dimensional hyper-molecules. We demonstrate these ideas in a prototype applied to synthetic data.

Continuously heterogeneous hyper-objects in cryo-EM and 3-D movies of many temporal dimensions

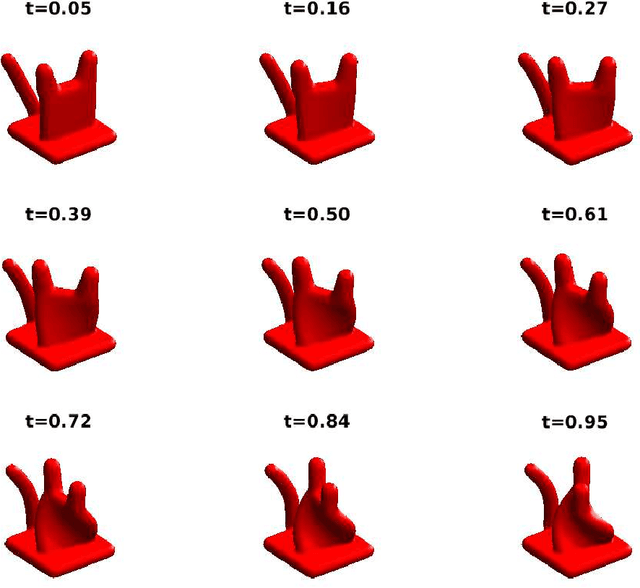
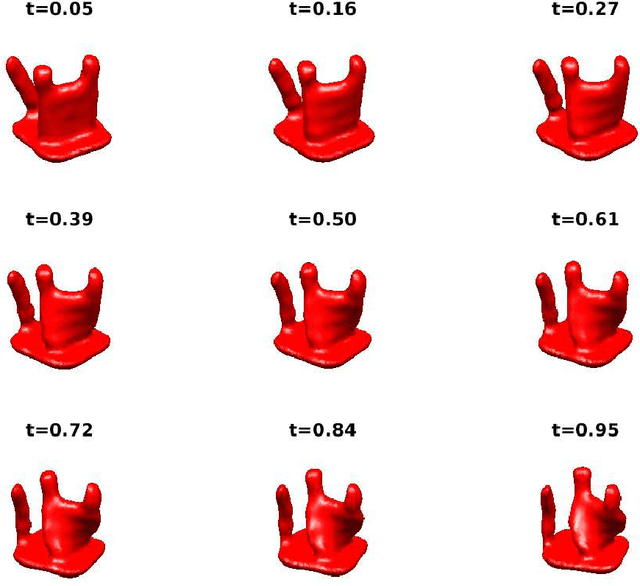
Single particle cryo-electron microscopy (EM) is an increasingly popular method for determining the 3-D structure of macromolecules from noisy 2-D images of single macromolecules whose orientations and positions are random and unknown. One of the great opportunities in cryo-EM is to recover the structure of macromolecules in heterogeneous samples, where multiple types or multiple conformations are mixed together. Indeed, in recent years, many tools have been introduced for the analysis of multiple discrete classes of molecules mixed together in a cryo-EM experiment. However, many interesting structures have a continuum of conformations which do not fit discrete models nicely; the analysis of such continuously heterogeneous models has remained a more elusive goal. In this manuscript, we propose to represent heterogeneous molecules and similar structures as higher dimensional objects. We generalize the basic operations used in many existing reconstruction algorithms, making our approach generic in the sense that, in principle, existing algorithms can be adapted to reconstruct those higher dimensional objects. As proof of concept, we present a prototype of a new algorithm which we use to solve simulated reconstruction problems.

A Representation Theory Perspective on Simultaneous Alignment and Classification

One of the difficulties in 3D reconstruction of molecules from images in single particle Cryo-Electron Microscopy (Cryo-EM), in addition to high levels of noise and unknown image orientations, is heterogeneity in samples: in many cases, the samples contain a mixture of molecules, or multiple conformations of one molecule. Many algorithms for the reconstruction of molecules from images in heterogeneous Cryo-EM experiments are based on iterative approximations of the molecules in a non-convex optimization that is prone to reaching suboptimal local minima. Other algorithms require an alignment in order to perform classification, or vice versa. The recently introduced Non-Unique Games framework provides a representation theoretic approach to studying problems of alignment over compact groups, and offers convex relaxations for alignment problems which are formulated as semidefinite programs (SDPs) with certificates of global optimality under certain circumstances. In this manuscript, we propose to extend Non-Unique Games to the problem of simultaneous alignment and classification with the goal of simultaneously classifying Cryo-EM images and aligning them within their respective classes. Our proposed approach can also be extended to the case of continuous heterogeneity.