Geometric Ergodicity in Modified Variations of Riemannian Manifold and Lagrangian Monte Carlo

Riemannian manifold Hamiltonian (RMHMC) and Lagrangian Monte Carlo (LMC) have emerged as powerful methods of Bayesian inference. Unlike Euclidean Hamiltonian Monte Carlo (EHMC) and the Metropolis-adjusted Langevin algorithm (MALA), the geometric ergodicity of these Riemannian algorithms has not been extensively studied. On the other hand, the manifold Metropolis-adjusted Langevin algorithm (MMALA) has recently been shown to exhibit geometric ergodicity under certain conditions. This work investigates the mixture of the LMC and RMHMC transition kernels with MMALA in order to equip the resulting method with an "inherited" geometric ergodicity theory. We motivate this mixture kernel based on an analogy between single-step HMC and MALA. We then proceed to evaluate the original and modified transition kernels on several benchmark Bayesian inference tasks.

Manifold Density Estimation via Generalized Dequantization

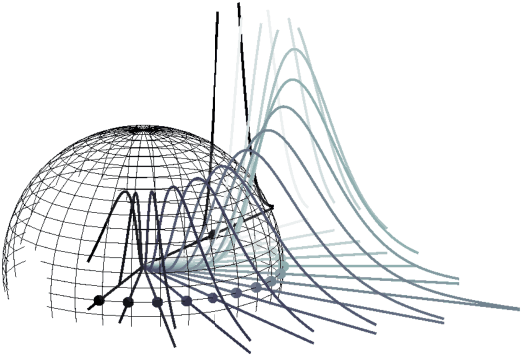
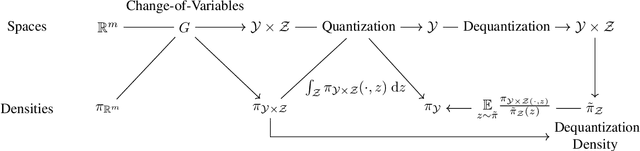
Density estimation is an important technique for characterizing distributions given observations. Much existing research on density estimation has focused on cases wherein the data lies in a Euclidean space. However, some kinds of data are not well-modeled by supposing that their underlying geometry is Euclidean. Instead, it can be useful to model such data as lying on a {\it manifold} with some known structure. For instance, some kinds of data may be known to lie on the surface of a sphere. We study the problem of estimating densities on manifolds. We propose a method, inspired by the literature on "dequantization," which we interpret through the lens of a coordinate transformation of an ambient Euclidean space and a smooth manifold of interest. Using methods from normalizing flows, we apply this method to the dequantization of smooth manifold structures in order to model densities on the sphere, tori, and the orthogonal group.

Magnetic Manifold Hamiltonian Monte Carlo

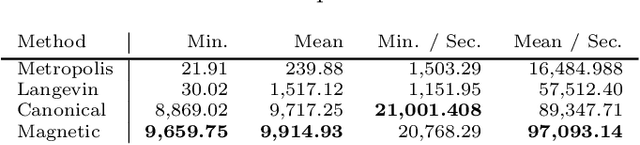
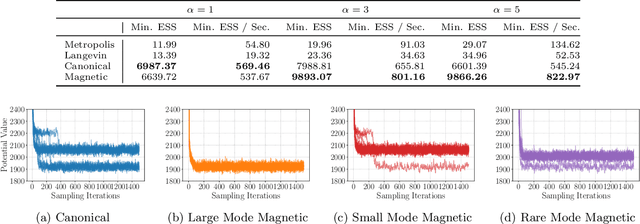
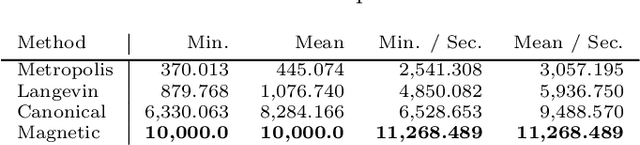
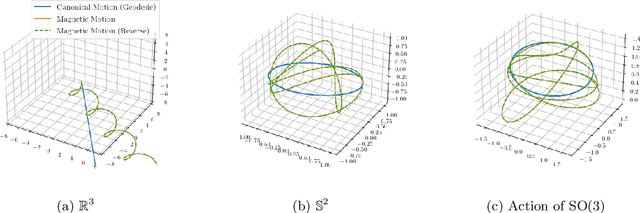
Markov chain Monte Carlo (MCMC) algorithms offer various strategies for sampling; the Hamiltonian Monte Carlo (HMC) family of samplers are MCMC algorithms which often exhibit improved mixing properties. The recently introduced magnetic HMC, a generalization of HMC motivated by the physics of particles influenced by magnetic field forces, has been demonstrated to improve the performance of HMC. In many applications, one wishes to sample from a distribution restricted to a constrained set, often manifested as an embedded manifold (for example, the surface of a sphere). We introduce magnetic manifold HMC, an HMC algorithm on embedded manifolds motivated by the physics of particles constrained to a manifold and moving under magnetic field forces. We discuss the theoretical properties of magnetic Hamiltonian dynamics on manifolds, and introduce a reversible and symplectic integrator for the HMC updates. We demonstrate that magnetic manifold HMC produces favorable sampling behaviors relative to the canonical variant of manifold-constrained HMC.

Non-Canonical Hamiltonian Monte Carlo

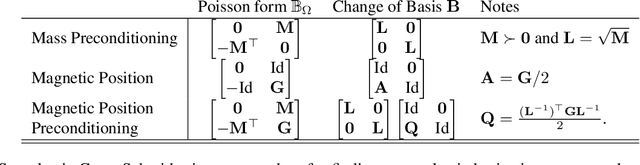
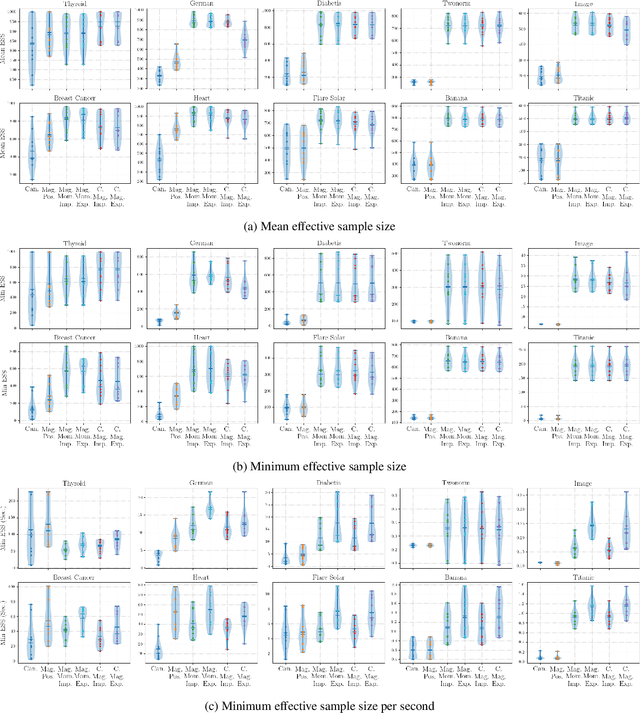
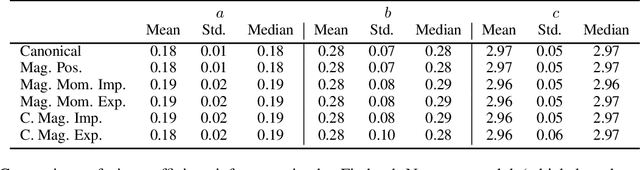
Hamiltonian Monte Carlo is typically based on the assumption of an underlying canonical symplectic structure. Numerical integrators designed for the canonical structure are incompatible with motion generated by non-canonical dynamics. These non-canonical dynamics, motivated by examples in physics and symplectic geometry, correspond to techniques such as preconditioning which are routinely used to improve algorithmic performance. Indeed, recently, a special case of non-canonical structure, magnetic Hamiltonian Monte Carlo, was demonstrated to provide advantageous sampling properties. We present a framework for Hamiltonian Monte Carlo using non-canonical symplectic structures. Our experimental results demonstrate sampling advantages associated to Hamiltonian Monte Carlo with non-canonical structure. To summarize our contributions: (i) we develop non-canonical HMC from foundations in symplectic geomtry; (ii) we construct an HMC procedure using implicit integration that satisfies the detailed balance; (iii) we propose to accelerate the sampling using an {\em approximate} explicit methodology; (iv) we study two novel, randomly-generated non-canonical structures: magnetic momentum and the coupled magnet structure, with implicit and explicit integration.