An Asynchronous Distributed Expectation Maximization Algorithm For Massive Data: The DEM Algorithm

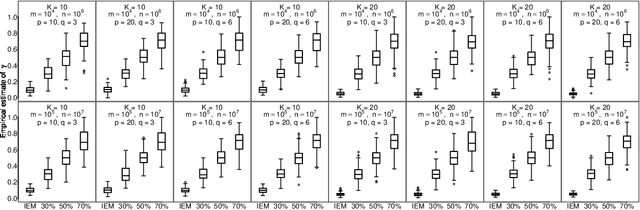
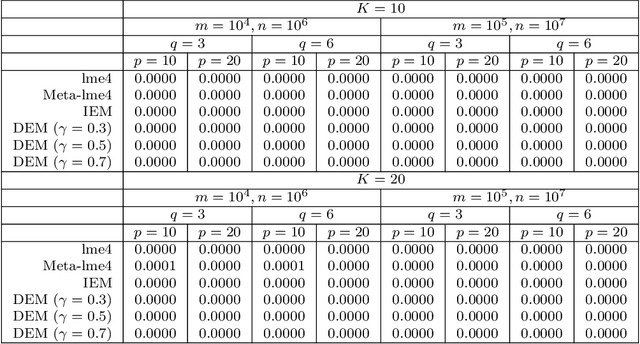
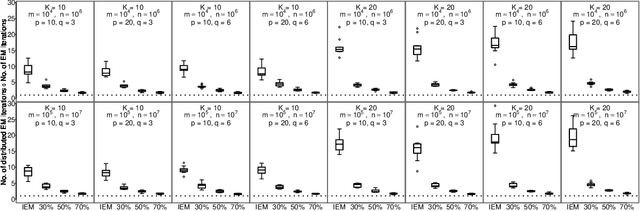
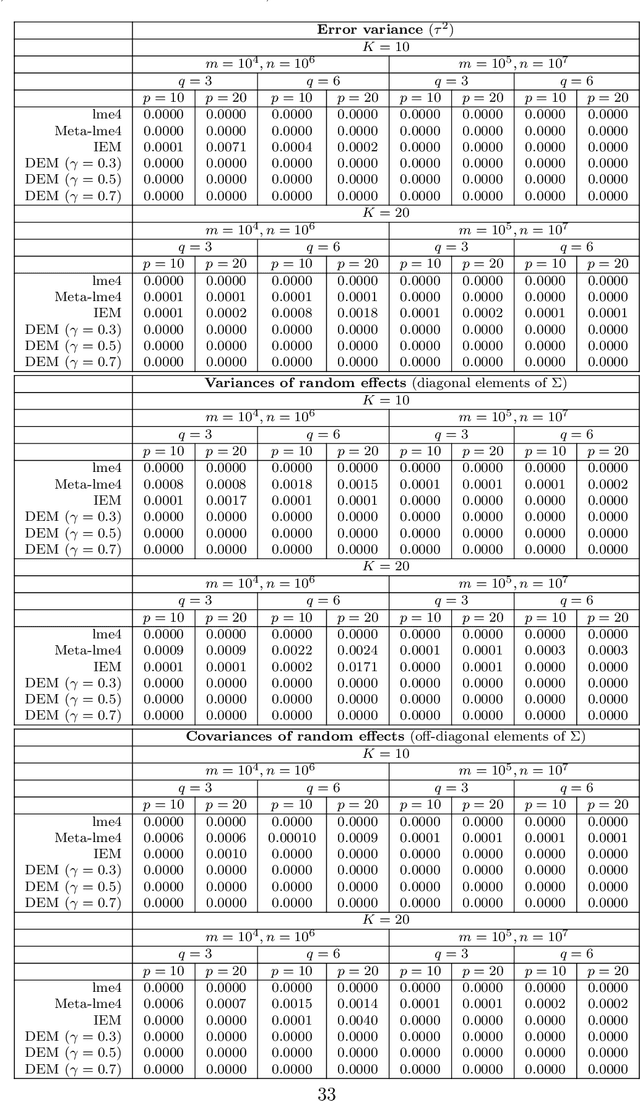
The family of Expectation-Maximization (EM) algorithms provides a general approach to fitting flexible models for large and complex data. The expectation (E) step of EM-type algorithms is time-consuming in massive data applications because it requires multiple passes through the full data. We address this problem by proposing an asynchronous and distributed generalization of the EM called the Distributed EM (DEM). Using DEM, existing EM-type algorithms are easily extended to massive data settings by exploiting the divide-and-conquer technique and widely available computing power, such as grid computing. The DEM algorithm reserves two groups of computing processes called \emph{workers} and \emph{managers} for performing the E step and the maximization step (M step), respectively. The samples are randomly partitioned into a large number of disjoint subsets and are stored on the worker processes. The E step of DEM algorithm is performed in parallel on all the workers, and every worker communicates its results to the managers at the end of local E step. The managers perform the M step after they have received results from a $\gamma$-fraction of the workers, where $\gamma$ is a fixed constant in $(0, 1]$. The sequence of parameter estimates generated by the DEM algorithm retains the attractive properties of EM: convergence of the sequence of parameter estimates to a local mode and linear global rate of convergence. Across diverse simulations focused on linear mixed-effects models, the DEM algorithm is significantly faster than competing EM-type algorithms while having a similar accuracy. The DEM algorithm maintains its superior empirical performance on a movie ratings database consisting of 10 million ratings.

The Dynamic ECME Algorithm

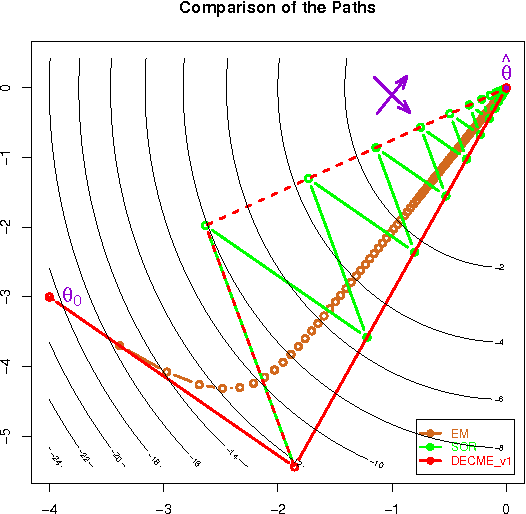
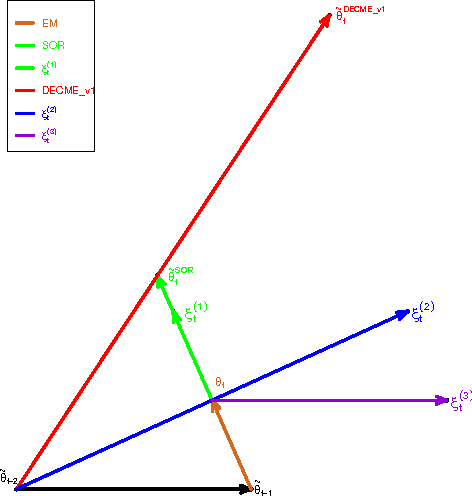
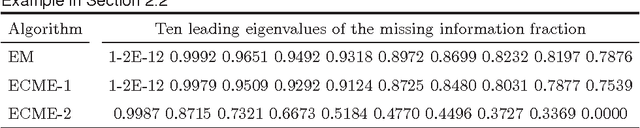
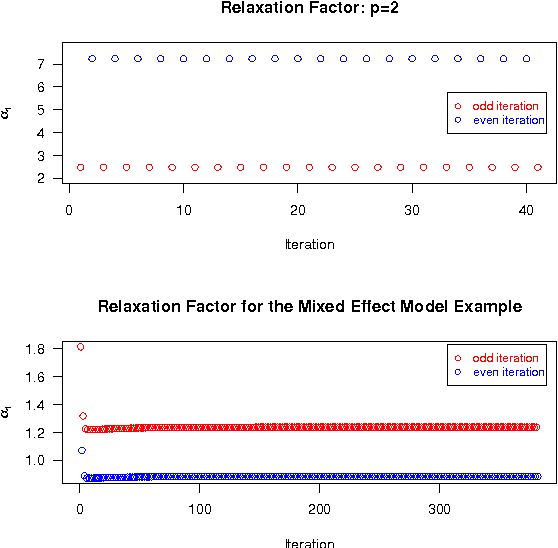
The ECME algorithm has proven to be an effective way of accelerating the EM algorithm for many problems. Recognising the limitation of using prefixed acceleration subspace in ECME, we propose the new Dynamic ECME (DECME) algorithm which allows the acceleration subspace to be chosen dynamically. Our investigation of an inefficient special case of DECME, the classical Successive Overrelaxation (SOR) method, leads to an efficient, simple, and widely applicable DECME implementation, called DECME_v1. The fast convergence of DECME_v1 is established by the theoretical result that, in a small neighbourhood of the maximum likelihood estimate (MLE), DECME_v1 is equivalent to a conjugate direction method. Numerical results show that DECME_v1 and its two variants are very stable and often converge faster than EM by a factor of one hundred in terms of number of iterations and a factor of thirty in terms of CPU time when EM is very slow.