An Asynchronous Distributed Expectation Maximization Algorithm For Massive Data: The DEM Algorithm
Paper and Code
Jun 20, 2018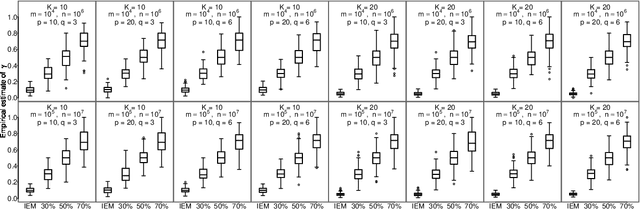
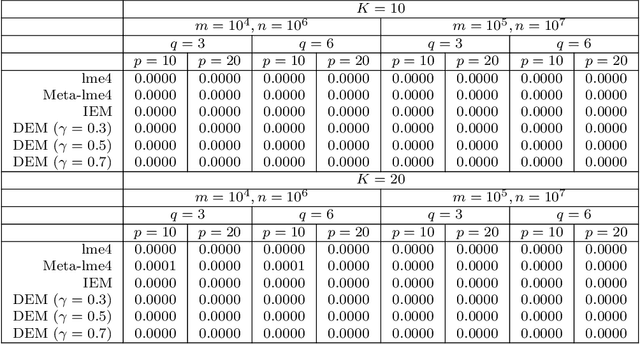
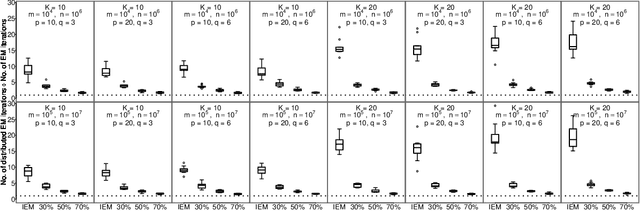
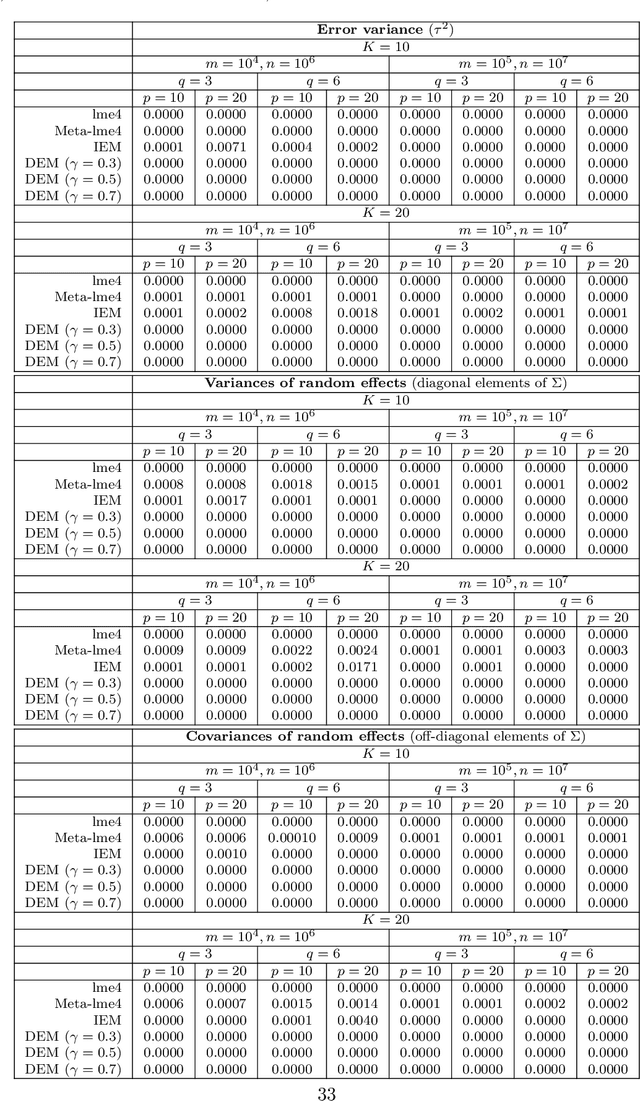
The family of Expectation-Maximization (EM) algorithms provides a general approach to fitting flexible models for large and complex data. The expectation (E) step of EM-type algorithms is time-consuming in massive data applications because it requires multiple passes through the full data. We address this problem by proposing an asynchronous and distributed generalization of the EM called the Distributed EM (DEM). Using DEM, existing EM-type algorithms are easily extended to massive data settings by exploiting the divide-and-conquer technique and widely available computing power, such as grid computing. The DEM algorithm reserves two groups of computing processes called \emph{workers} and \emph{managers} for performing the E step and the maximization step (M step), respectively. The samples are randomly partitioned into a large number of disjoint subsets and are stored on the worker processes. The E step of DEM algorithm is performed in parallel on all the workers, and every worker communicates its results to the managers at the end of local E step. The managers perform the M step after they have received results from a $\gamma$-fraction of the workers, where $\gamma$ is a fixed constant in $(0, 1]$. The sequence of parameter estimates generated by the DEM algorithm retains the attractive properties of EM: convergence of the sequence of parameter estimates to a local mode and linear global rate of convergence. Across diverse simulations focused on linear mixed-effects models, the DEM algorithm is significantly faster than competing EM-type algorithms while having a similar accuracy. The DEM algorithm maintains its superior empirical performance on a movie ratings database consisting of 10 million ratings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge