Numerical Approximation of Andrews Plots with Optimal Spatial-Spectral Smoothing

Andrews plots provide aesthetically pleasant visualizations of high-dimensional datasets. This work proves that Andrews plots (when defined in terms of the principal component scores of a dataset) are optimally ``smooth'' on average, and solve an infinite-dimensional quadratic minimization program over the set of linear isometries from the Euclidean data space to $L^2([0,1])$. By building technical machinery that characterizes the solutions to general infinite-dimensional quadratic minimization programs over linear isometries, we further show that the solution set is (in the generic case) a manifold. To avoid the ambiguities presented by this manifold of solutions, we add ``spectral smoothing'' terms to the infinite-dimensional optimization program to induce Andrews plots with optimal spatial-spectral smoothing. We characterize the (generic) set of solutions to this program and prove that the resulting plots admit efficient numerical approximations. These spatial-spectral smooth Andrews plots tend to avoid some ``visual clutter'' that arises due to the oscillation of trigonometric polynomials.

Filament Plots for Data Visualization

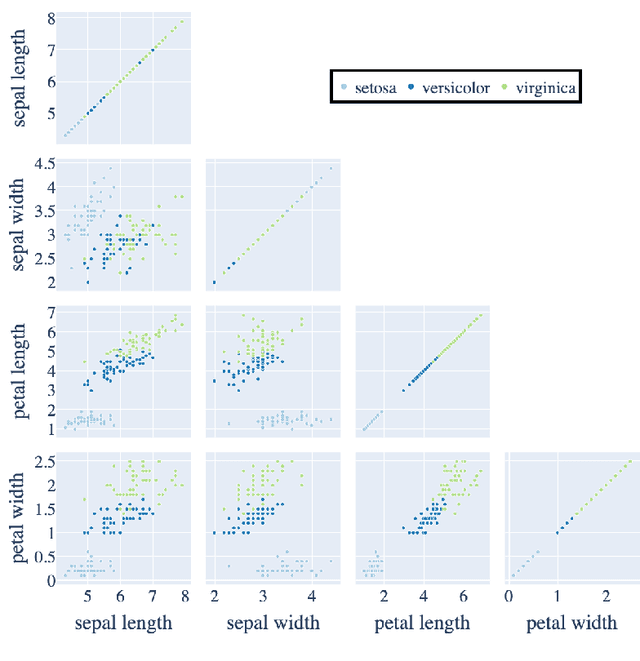
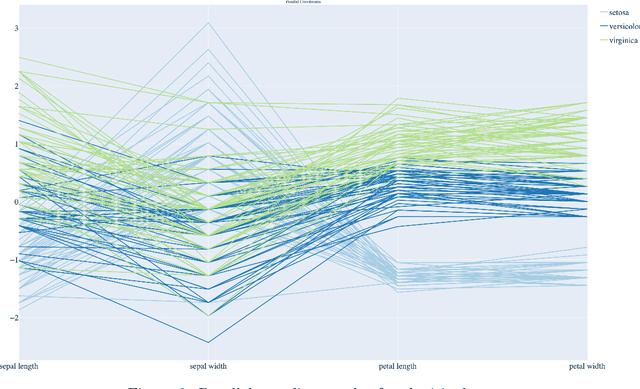
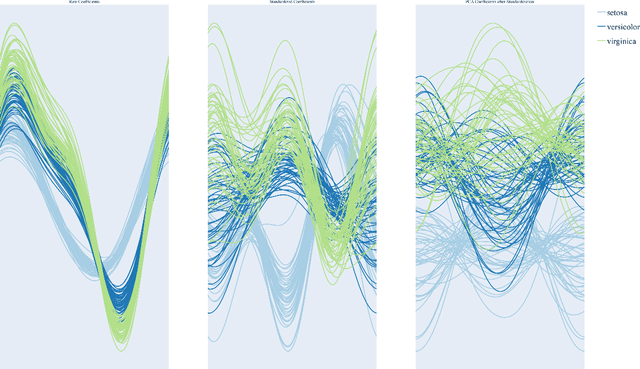
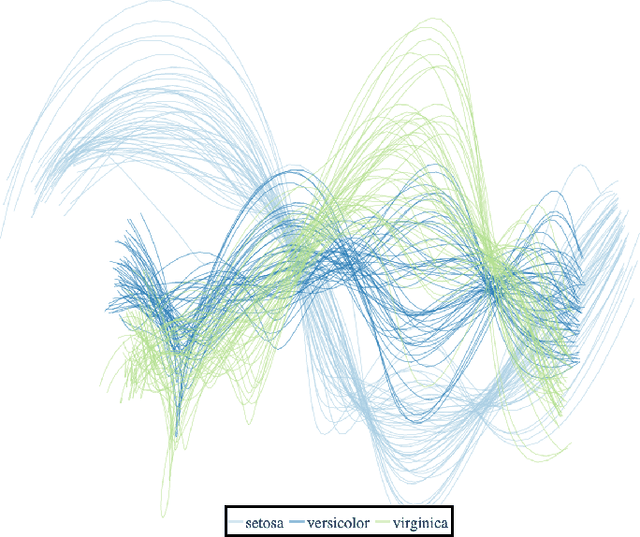
We construct a computationally inexpensive 3D extension of Andrew's plots by considering curves generated by Frenet-Serret equations and induced by optimally smooth 2D Andrew's plots. We consider linear isometries from a Euclidean data space to infinite dimensional spaces of 2D curves, and parametrize the linear isometries that produce (on average) optimally smooth curves over a given dataset. This set of optimal isometries admits many degrees of freedom, and (using recent results on generalized Gauss sums) we identify a particular a member of this set which admits an asymptotic projective "tour" property. Finally, we consider the unit-length 3D curves (filaments) induced by these 2D Andrew's plots, where the linear isometry property preserves distances as "relative total square curvatures". This work concludes by illustrating filament plots for several datasets. Code is available at https://github.com/n8epi/filaments

Distributed Statistical Estimation and Rates of Convergence in Normal Approximation

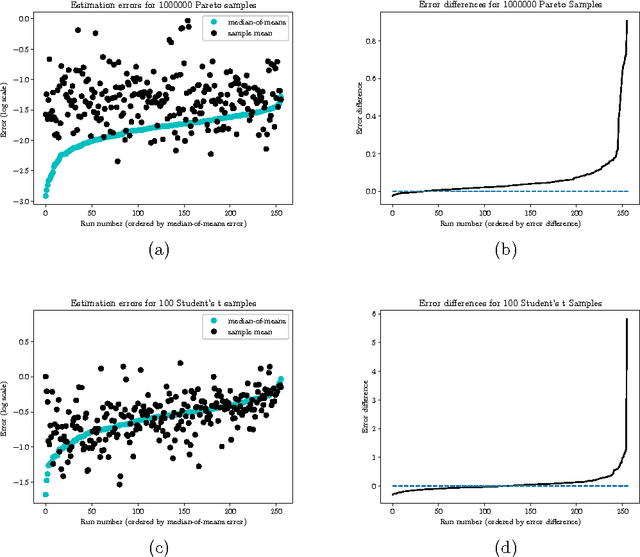
This paper presents a class of new algorithms for distributed statistical estimation that exploit divide-and-conquer approach. We show that one of the key benefits of the divide-and-conquer strategy is robustness, an important characteristic for large distributed systems. We establish connections between performance of these distributed algorithms and the rates of convergence in normal approximation, and prove non-asymptotic deviations guarantees, as well as limit theorems, for the resulting estimators. Our techniques are illustrated through several examples: in particular, we obtain new results for the median-of-means estimator, as well as provide performance guarantees for distributed maximum likelihood estimation.

Topological and Statistical Behavior Classifiers for Tracking Applications

We introduce the first unified theory for target tracking using Multiple Hypothesis Tracking, Topological Data Analysis, and machine learning. Our string of innovations are 1) robust topological features are used to encode behavioral information, 2) statistical models are fitted to distributions over these topological features, and 3) the target type classification methods of Wigren and Bar Shalom et al. are employed to exploit the resulting likelihoods for topological features inside of the tracking procedure. To demonstrate the efficacy of our approach, we test our procedure on synthetic vehicular data generated by the Simulation of Urban Mobility package.