Filament Plots for Data Visualization
Paper and Code
Jul 20, 2021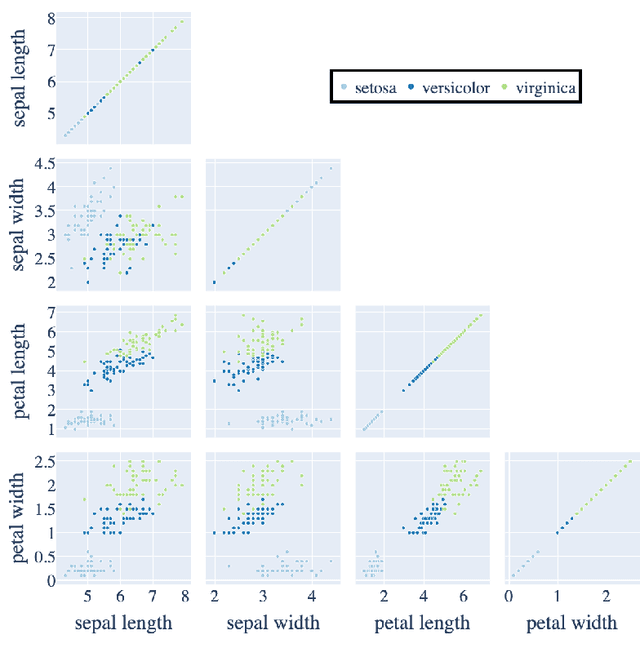
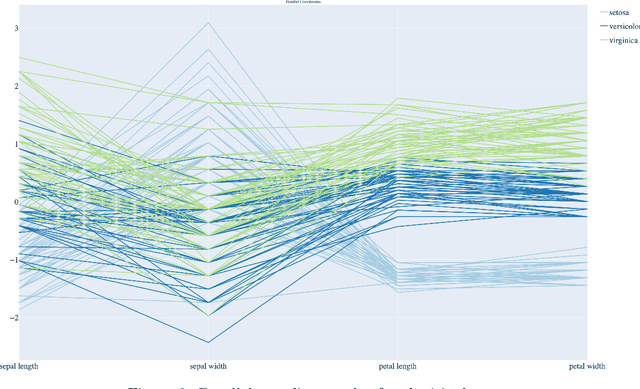
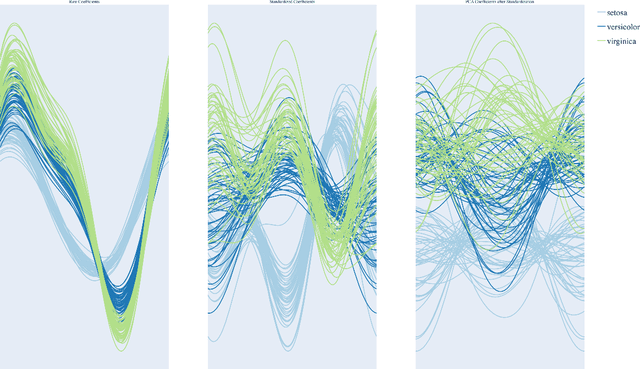
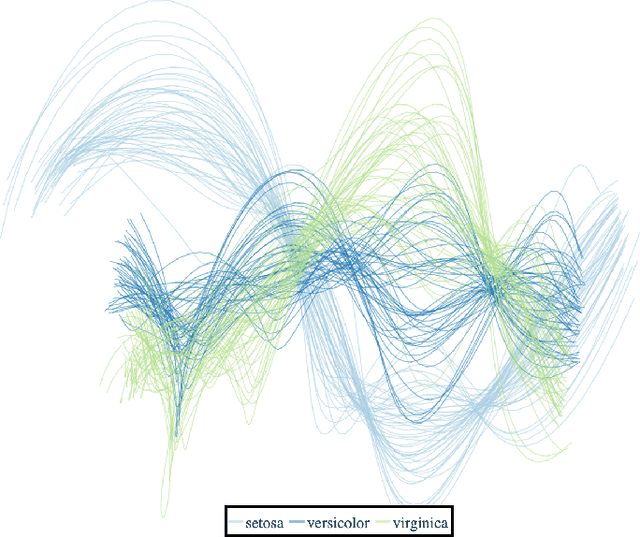
We construct a computationally inexpensive 3D extension of Andrew's plots by considering curves generated by Frenet-Serret equations and induced by optimally smooth 2D Andrew's plots. We consider linear isometries from a Euclidean data space to infinite dimensional spaces of 2D curves, and parametrize the linear isometries that produce (on average) optimally smooth curves over a given dataset. This set of optimal isometries admits many degrees of freedom, and (using recent results on generalized Gauss sums) we identify a particular a member of this set which admits an asymptotic projective "tour" property. Finally, we consider the unit-length 3D curves (filaments) induced by these 2D Andrew's plots, where the linear isometry property preserves distances as "relative total square curvatures". This work concludes by illustrating filament plots for several datasets. Code is available at https://github.com/n8epi/filaments
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge