Distributed Statistical Estimation and Rates of Convergence in Normal Approximation
Paper and Code
Aug 27, 2018
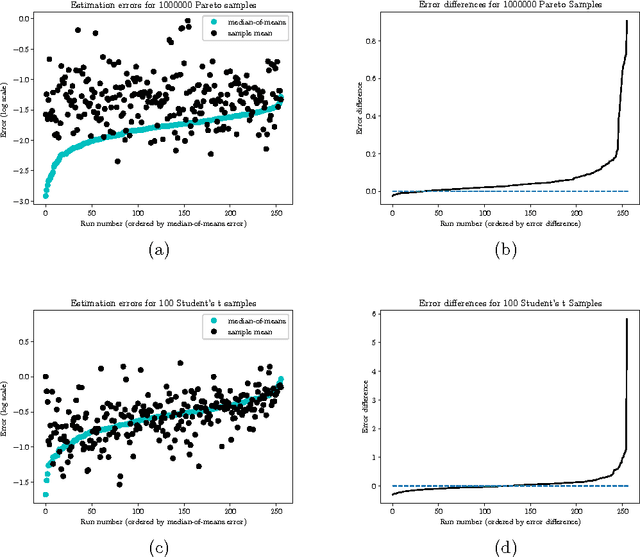
This paper presents a class of new algorithms for distributed statistical estimation that exploit divide-and-conquer approach. We show that one of the key benefits of the divide-and-conquer strategy is robustness, an important characteristic for large distributed systems. We establish connections between performance of these distributed algorithms and the rates of convergence in normal approximation, and prove non-asymptotic deviations guarantees, as well as limit theorems, for the resulting estimators. Our techniques are illustrated through several examples: in particular, we obtain new results for the median-of-means estimator, as well as provide performance guarantees for distributed maximum likelihood estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge