Ask for More Than Bayes Optimal: A Theory of Indecisions for Classification

Selective classification frameworks are useful tools for automated decision making in highly risky scenarios, since they allow for a classifier to only make highly confident decisions, while abstaining from making a decision when it is not confident enough to do so, which is otherwise known as an indecision. For a given level of classification accuracy, we aim to make as many decisions as possible. For many problems, this can be achieved without abstaining from making decisions. But when the problem is hard enough, we show that we can still control the misclassification rate of a classifier up to any user specified level, while only abstaining from the minimum necessary amount of decisions, even if this level of misclassification is smaller than the Bayes optimal error rate. In many problem settings, the user could obtain a dramatic decrease in misclassification while only paying a comparatively small price in terms of indecisions.

Asymmetric error control under imperfect supervision: a label-noise-adjusted Neyman-Pearson umbrella algorithm

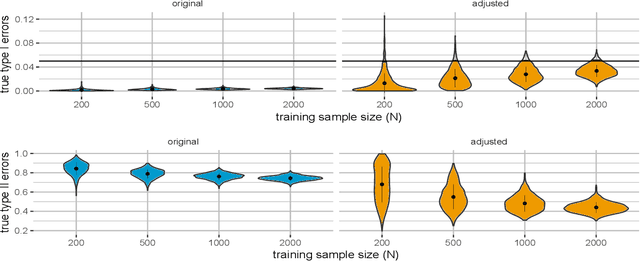
Label noise in data has long been an important problem in supervised learning applications as it affects the effectiveness of many widely used classification methods. Recently, important real-world applications, such as medical diagnosis and cybersecurity, have generated renewed interest in the Neyman-Pearson (NP) classification paradigm, which constrains the more severe type of error (e.g., the type I error) under a preferred level while minimizing the other (e.g., the type II error). However, there has been little research on the NP paradigm under label noise. It is somewhat surprising that even when common NP classifiers ignore the label noise in the training stage, they are still able to control the type I error with high probability. However, the price they pay is excessive conservativeness of the type I error and hence a significant drop in power (i.e., $1 - $ type II error). Assuming that domain experts provide lower bounds on the corruption severity, we propose the first theory-backed algorithm that adapts most state-of-the-art classification methods to the training label noise under the NP paradigm. The resulting classifiers not only control the type I error with high probability under the desired level but also improve power.