Shunan Yao
Asymmetric error control under imperfect supervision: a label-noise-adjusted Neyman-Pearson umbrella algorithm
Dec 01, 2021

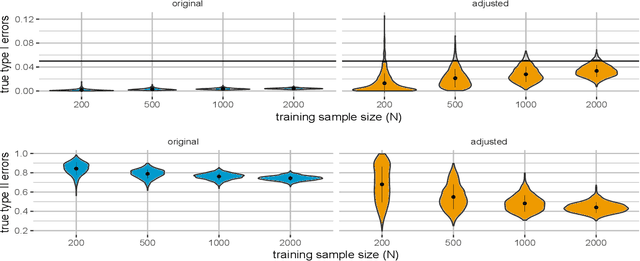

Abstract:Label noise in data has long been an important problem in supervised learning applications as it affects the effectiveness of many widely used classification methods. Recently, important real-world applications, such as medical diagnosis and cybersecurity, have generated renewed interest in the Neyman-Pearson (NP) classification paradigm, which constrains the more severe type of error (e.g., the type I error) under a preferred level while minimizing the other (e.g., the type II error). However, there has been little research on the NP paradigm under label noise. It is somewhat surprising that even when common NP classifiers ignore the label noise in the training stage, they are still able to control the type I error with high probability. However, the price they pay is excessive conservativeness of the type I error and hence a significant drop in power (i.e., $1 - $ type II error). Assuming that domain experts provide lower bounds on the corruption severity, we propose the first theory-backed algorithm that adapts most state-of-the-art classification methods to the training label noise under the NP paradigm. The resulting classifiers not only control the type I error with high probability under the desired level but also improve power.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge