A Note on Coding and Standardization of Categorical Variables in Group Lasso Regression

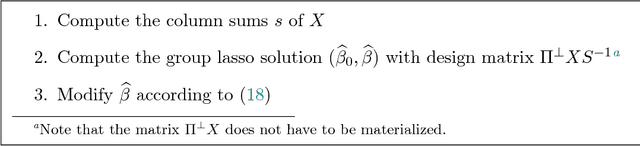
Categorical regressor variables are usually handled by introducing a set of indicator variables, and imposing a linear constraint to ensure identifiability in the presence of an intercept, or equivalently, using one of various coding schemes. As proposed in Yuan and Lin [J. R. Statist. Soc. B, 68 (2006), 49-67], the group lasso is a natural and computationally convenient approach to perform variable selection in settings with categorical covariates. As pointed out by Simon and Tibshirani [Stat. Sin., 22 (2011), 983-1001], "standardization" by means of block-wise orthonormalization of column submatrices each corresponding to one group of variables can substantially boost performance. In this note, we study the aspect of standardization for the special case of categorical predictors in detail. The main result is that orthonormalization is not required; column-wise scaling of the design matrix followed by re-scaling and centering of the coefficients is shown to have exactly the same effect. Similar reductions can be achieved in the case of interactions. The extension to the so-called sparse group lasso, which additionally promotes within-group sparsity, is considered as well. The importance of proper standardization is illustrated via extensive simulations.