Asymmetric Multiresolution Matrix Factorization

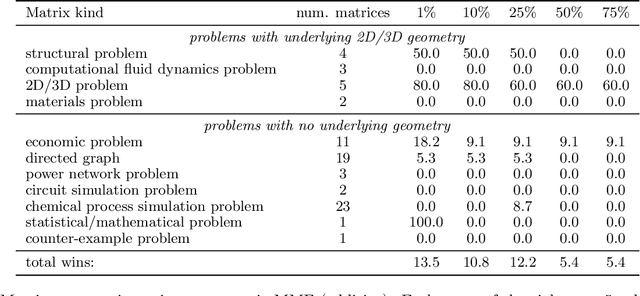
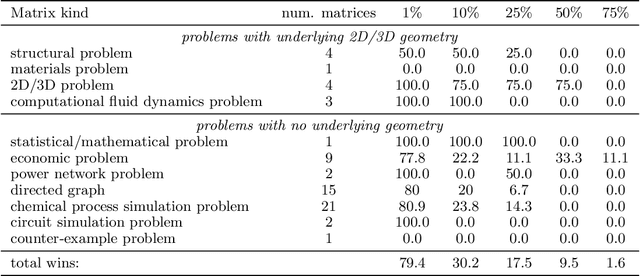
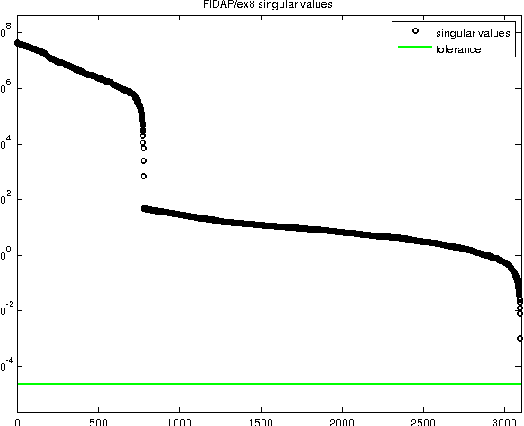
Multiresolution Matrix Factorization (MMF) was recently introduced as an alternative to the dominant low-rank paradigm in order to capture structure in matrices at multiple different scales. Using ideas from multiresolution analysis (MRA), MMF teased out hierarchical structure in symmetric matrices by constructing a sequence of wavelet bases. While effective for such matrices, there is plenty of data that is more naturally represented as nonsymmetric matrices (e.g. directed graphs), but nevertheless has similar hierarchical structure. In this paper, we explore techniques for extending MMF to any square matrix. We validate our approach on numerous matrix compression tasks, demonstrating its efficacy compared to low-rank methods. Moreover, we also show that a combined low-rank and MMF approach, which amounts to removing a small global-scale component of the matrix and then extracting hierarchical structure from the residual, is even more effective than each of the two complementary methods for matrix compression.

K For The Price Of 1: Parameter Efficient Multi-task And Transfer Learning

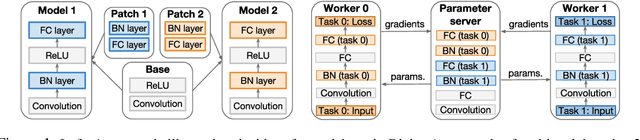
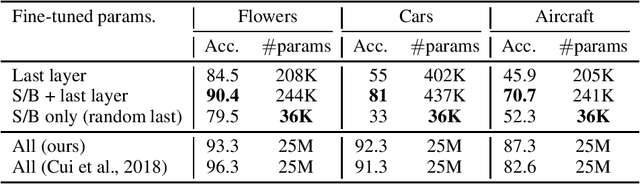
We introduce a novel method that enables parameter-efficient transfer and multitask learning. The basic approach is to allow a model patch - a small set of parameters - to specialize to each task, instead of fine-tuning the last layer or the entire network. For instance, we show that learning a set of scales and biases allows a network to learn a completely different embedding that could be used for different tasks (such as converting an SSD detection model into a 1000-class classification model while reusing 98% of parameters of the feature extractor). Similarly, we show that re-learning the existing low-parameter layers (such as depth-wise convolutions) also improves accuracy significantly. Our approach allows both simultaneous (multi-task) learning as well as sequential transfer learning wherein we adapt pretrained networks to solve new problems. For multi-task learning, despite using much fewer parameters than traditional logits-only fine-tuning, we match single-task-based performance.

Did the Model Understand the Question?

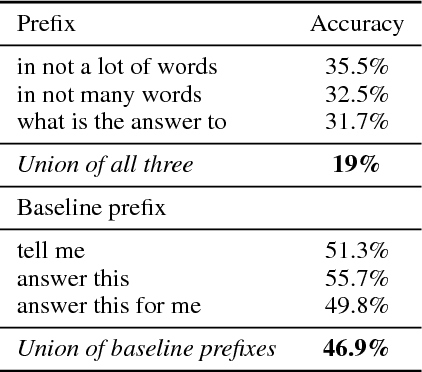
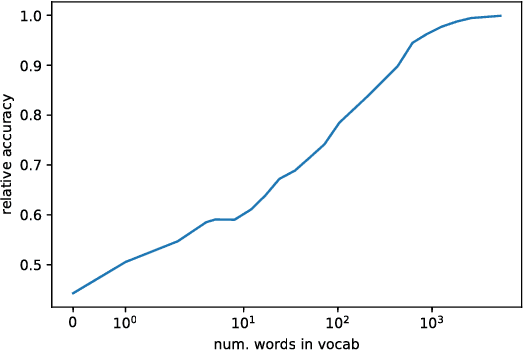
We analyze state-of-the-art deep learning models for three tasks: question answering on (1) images, (2) tables, and (3) passages of text. Using the notion of \emph{attribution} (word importance), we find that these deep networks often ignore important question terms. Leveraging such behavior, we perturb questions to craft a variety of adversarial examples. Our strongest attacks drop the accuracy of a visual question answering model from $61.1\%$ to $19\%$, and that of a tabular question answering model from $33.5\%$ to $3.3\%$. Additionally, we show how attributions can strengthen attacks proposed by Jia and Liang (2017) on paragraph comprehension models. Our results demonstrate that attributions can augment standard measures of accuracy and empower investigation of model performance. When a model is accurate but for the wrong reasons, attributions can surface erroneous logic in the model that indicates inadequacies in the test data.

It was the training data pruning too!

We study the current best model (KDG) for question answering on tabular data evaluated over the WikiTableQuestions dataset. Previous ablation studies performed against this model attributed the model's performance to certain aspects of its architecture. In this paper, we find that the model's performance also crucially depends on a certain pruning of the data used to train the model. Disabling the pruning step drops the accuracy of the model from 43.3% to 36.3%. The large impact on the performance of the KDG model suggests that the pruning may be a useful pre-processing step in training other semantic parsers as well.

Tight Continuous Relaxation of the Balanced $k$-Cut Problem

Spectral Clustering as a relaxation of the normalized/ratio cut has become one of the standard graph-based clustering methods. Existing methods for the computation of multiple clusters, corresponding to a balanced $k$-cut of the graph, are either based on greedy techniques or heuristics which have weak connection to the original motivation of minimizing the normalized cut. In this paper we propose a new tight continuous relaxation for any balanced $k$-cut problem and show that a related recently proposed relaxation is in most cases loose leading to poor performance in practice. For the optimization of our tight continuous relaxation we propose a new algorithm for the difficult sum-of-ratios minimization problem which achieves monotonic descent. Extensive comparisons show that our method outperforms all existing approaches for ratio cut and other balanced $k$-cut criteria.