Equilibrium Aggregation: Encoding Sets via Optimization

Processing sets or other unordered, potentially variable-sized inputs in neural networks is usually handled by \emph{aggregating} a number of input tensors into a single representation. While a number of aggregation methods already exist from simple sum pooling to multi-head attention, they are limited in their representational power both from theoretical and empirical perspectives. On the search of a principally more powerful aggregation strategy, we propose an optimization-based method called Equilibrium Aggregation. We show that many existing aggregation methods can be recovered as special cases of Equilibrium Aggregation and that it is provably more efficient in some important cases. Equilibrium Aggregation can be used as a drop-in replacement in many existing architectures and applications. We validate its efficiency on three different tasks: median estimation, class counting, and molecular property prediction. In all experiments, Equilibrium Aggregation achieves higher performance than the other aggregation techniques we test.

Universal Approximation of Functions on Sets

Modelling functions of sets, or equivalently, permutation-invariant functions, is a long-standing challenge in machine learning. Deep Sets is a popular method which is known to be a universal approximator for continuous set functions. We provide a theoretical analysis of Deep Sets which shows that this universal approximation property is only guaranteed if the model's latent space is sufficiently high-dimensional. If the latent space is even one dimension lower than necessary, there exist piecewise-affine functions for which Deep Sets performs no better than a na\"ive constant baseline, as judged by worst-case error. Deep Sets may be viewed as the most efficient incarnation of the Janossy pooling paradigm. We identify this paradigm as encompassing most currently popular set-learning methods. Based on this connection, we discuss the implications of our results for set learning more broadly, and identify some open questions on the universality of Janossy pooling in general.

E(n) Equivariant Normalizing Flows

This paper introduces a generative model equivariant to Euclidean symmetries: E(n) Equivariant Normalizing Flows (E-NFs). To construct E-NFs, we take the discriminative E(n) graph neural networks and integrate them as a differential equation to obtain an invertible equivariant function: a continuous-time normalizing flow. We demonstrate that E-NFs considerably outperform baselines and existing methods from the literature on particle systems such as DW4 and LJ13, and on molecules from QM9 in terms of log-likelihood. To the best of our knowledge, this is the first flow that jointly generates molecule features and positions in 3D.

Iterative SE(3)-Transformers

When manipulating three-dimensional data, it is possible to ensure that rotational and translational symmetries are respected by applying so-called SE(3)-equivariant models. Protein structure prediction is a prominent example of a task which displays these symmetries. Recent work in this area has successfully made use of an SE(3)-equivariant model, applying an iterative SE(3)-equivariant attention mechanism. Motivated by this application, we implement an iterative version of the SE(3)-Transformer, an SE(3)-equivariant attention-based model for graph data. We address the additional complications which arise when applying the SE(3)-Transformer in an iterative fashion, compare the iterative and single-pass versions on a toy problem, and consider why an iterative model may be beneficial in some problem settings. We make the code for our implementation available to the community.

SE(3)-Transformers: 3D Roto-Translation Equivariant Attention Networks

We introduce the SE(3)-Transformer, a variant of the self-attention module for 3D point clouds, which is equivariant under continuous 3D roto-translations. Equivariance is important to ensure stable and predictable performance in the presence of nuisance transformations of the data input. A positive corollary of equivariance is increased weight-tying within the model, leading to fewer trainable parameters and thus decreased sample complexity (i.e. we need less training data). The SE(3)-Transformer leverages the benefits of self-attention to operate on large point clouds with varying number of points, while guaranteeing SE(3)-equivariance for robustness. We evaluate our model on a toy $N$-body particle simulation dataset, showcasing the robustness of the predictions under rotations of the input. We further achieve competitive performance on two real-world datasets, ScanObjectNN and QM9. In all cases, our model outperforms a strong, non-equivariant attention baseline and an equivariant model without attention.

End-to-end Recurrent Multi-Object Tracking and Trajectory Prediction with Relational Reasoning

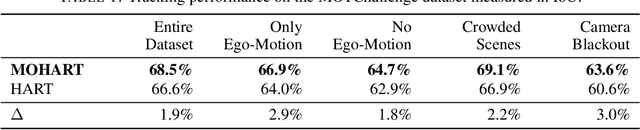
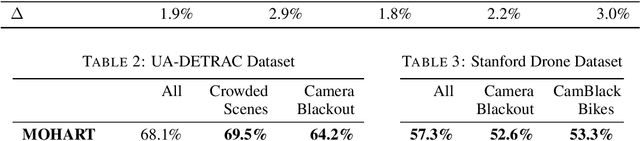
The majority of contemporary object-tracking approaches used in autonomous vehicles do not model interactions between objects. This contrasts with the fact that objects' paths are not independent: a cyclist might abruptly deviate from a previously planned trajectory in order to avoid colliding with a car. Building upon HART, a neural, class-agnostic single-object tracker, we introduce a multi-object tracking method MOHART capable of relational reasoning. Importantly, the entire system, including the understanding of interactions and relations between objects, is class-agnostic and learned simultaneously in an end-to-end fashion. We find that the addition of relational-reasoning capabilities to HART leads to consistent performance gains in tracking as well as future trajectory prediction on several real-world datasets (MOTChallenge, UA-DETRAC, and Stanford Drone dataset), particularly in the presence of ego-motion, occlusions, crowded scenes, and faulty sensor inputs. Finally, based on controlled simulations, we propose that a comparison of MOHART and HART may be used as a novel way to measure the degree to which the objects in a video depend upon each other as they move together through time.

On the Limitations of Representing Functions on Sets

Recent work on the representation of functions on sets has considered the use of summation in a latent space to enforce permutation invariance. In particular, it has been conjectured that the dimension of this latent space may remain fixed as the cardinality of the sets under consideration increases. However, we demonstrate that the analysis leading to this conjecture requires mappings which are highly discontinuous and argue that this is only of limited practical use. Motivated by this observation, we prove that an implementation of this model via continuous mappings (as provided by e.g. neural networks or Gaussian processes) actually imposes a constraint on the dimensionality of the latent space. Practical universal function representation for set inputs can only be achieved with a latent dimension at least the size of the maximum number of input elements.

ShapeStacks: Learning Vision-Based Physical Intuition for Generalised Object Stacking

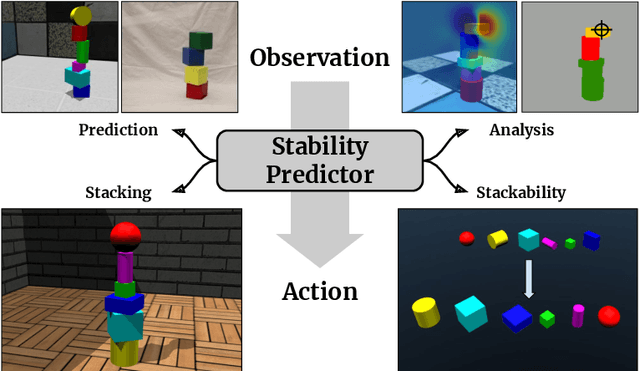
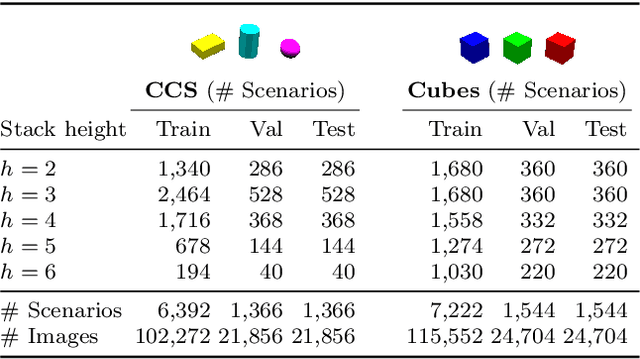
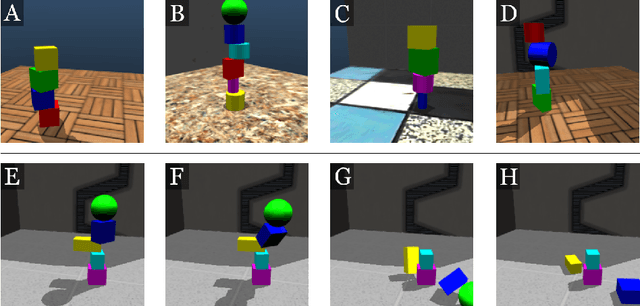
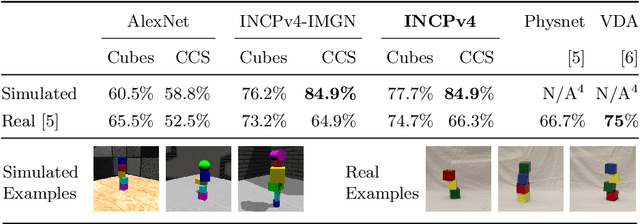
Physical intuition is pivotal for intelligent agents to perform complex tasks. In this paper we investigate the passive acquisition of an intuitive understanding of physical principles as well as the active utilisation of this intuition in the context of generalised object stacking. To this end, we provide: a simulation-based dataset featuring 20,000 stack configurations composed of a variety of elementary geometric primitives richly annotated regarding semantics and structural stability. We train visual classifiers for binary stability prediction on the ShapeStacks data and scrutinise their learned physical intuition. Due to the richness of the training data our approach also generalises favourably to real-world scenarios achieving state-of-the-art stability prediction on a publicly available benchmark of block towers. We then leverage the physical intuition learned by our model to actively construct stable stacks and observe the emergence of an intuitive notion of stackability - an inherent object affordance - induced by the active stacking task. Our approach performs well even in challenging conditions where it considerably exceeds the stack height observed during training or in cases where initially unstable structures must be stabilised via counterbalancing.

Neural Stethoscopes: Unifying Analytic, Auxiliary and Adversarial Network Probing

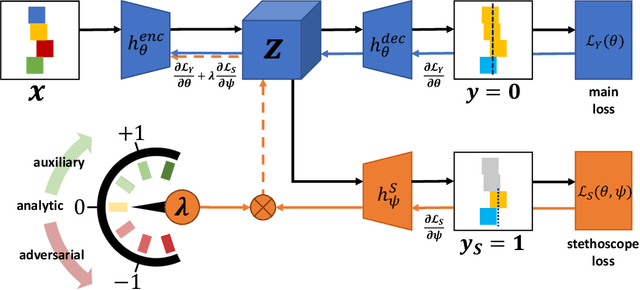
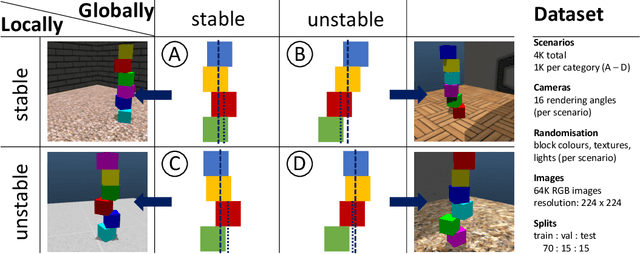
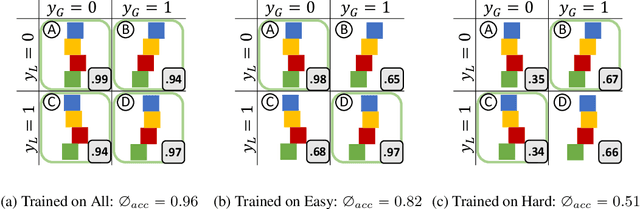
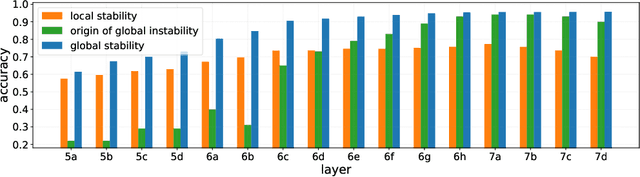
Model interpretability and systematic, targeted model adaptation present central tenets in machine learning for addressing limited or biased datasets. In this paper, we introduce neural stethoscopes as a framework for quantifying the degree of importance of specific factors of influence in deep networks as well as for actively promoting and suppressing information as appropriate. In doing so we unify concepts from multitask learning as well as training with auxiliary and adversarial losses. We showcase the efficacy of neural stethoscopes in an intuitive physics domain. Specifically, we investigate the challenge of visually predicting stability of block towers and demonstrate that the network uses visual cues which makes it susceptible to biases in the dataset. Through the use of stethoscopes we interrogate the accessibility of specific information throughout the network stack and show that we are able to actively de-bias network predictions as well as enhance performance via suitable auxiliary and adversarial stethoscope losses.