Universal Approximation of Functions on Sets

Modelling functions of sets, or equivalently, permutation-invariant functions, is a long-standing challenge in machine learning. Deep Sets is a popular method which is known to be a universal approximator for continuous set functions. We provide a theoretical analysis of Deep Sets which shows that this universal approximation property is only guaranteed if the model's latent space is sufficiently high-dimensional. If the latent space is even one dimension lower than necessary, there exist piecewise-affine functions for which Deep Sets performs no better than a na\"ive constant baseline, as judged by worst-case error. Deep Sets may be viewed as the most efficient incarnation of the Janossy pooling paradigm. We identify this paradigm as encompassing most currently popular set-learning methods. Based on this connection, we discuss the implications of our results for set learning more broadly, and identify some open questions on the universality of Janossy pooling in general.

Iterative SE(3)-Transformers

When manipulating three-dimensional data, it is possible to ensure that rotational and translational symmetries are respected by applying so-called SE(3)-equivariant models. Protein structure prediction is a prominent example of a task which displays these symmetries. Recent work in this area has successfully made use of an SE(3)-equivariant model, applying an iterative SE(3)-equivariant attention mechanism. Motivated by this application, we implement an iterative version of the SE(3)-Transformer, an SE(3)-equivariant attention-based model for graph data. We address the additional complications which arise when applying the SE(3)-Transformer in an iterative fashion, compare the iterative and single-pass versions on a toy problem, and consider why an iterative model may be beneficial in some problem settings. We make the code for our implementation available to the community.

Correlation of Auroral Dynamics and GNSS Scintillation with an Autoencoder

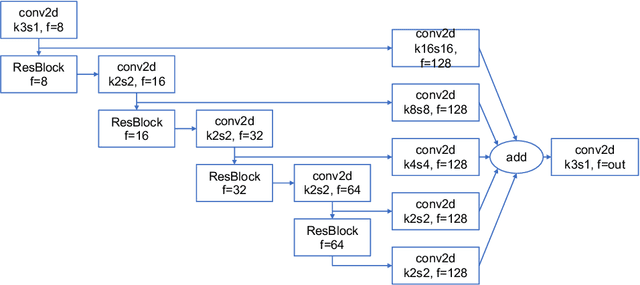
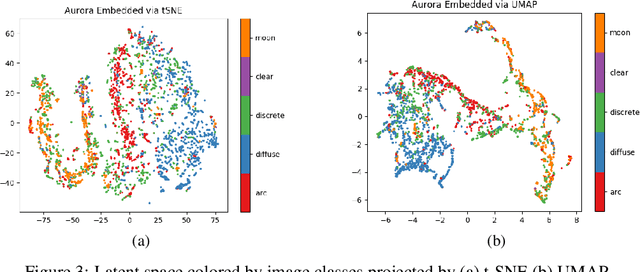
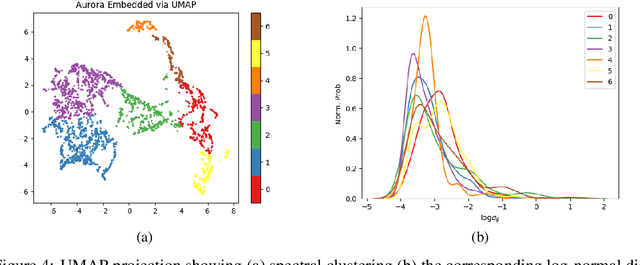
High energy particles originating from solar activity travel along the the Earth's magnetic field and interact with the atmosphere around the higher latitudes. These interactions often manifest as aurora in the form of visible light in the Earth's ionosphere. These interactions also result in irregularities in the electron density, which cause disruptions in the amplitude and phase of the radio signals from the Global Navigation Satellite Systems (GNSS), known as 'scintillation'. In this paper we use a multi-scale residual autoencoder (Res-AE) to show the correlation between specific dynamic structures of the aurora and the magnitude of the GNSS phase scintillations ($\sigma_{\phi}$). Auroral images are encoded in a lower dimensional feature space using the Res-AE, which in turn are clustered with t-SNE and UMAP. Both methods produce similar clusters, and specific clusters demonstrate greater correlations with observed phase scintillations. Our results suggest that specific dynamic structures of auroras are highly correlated with GNSS phase scintillations.

Prediction of GNSS Phase Scintillations: A Machine Learning Approach

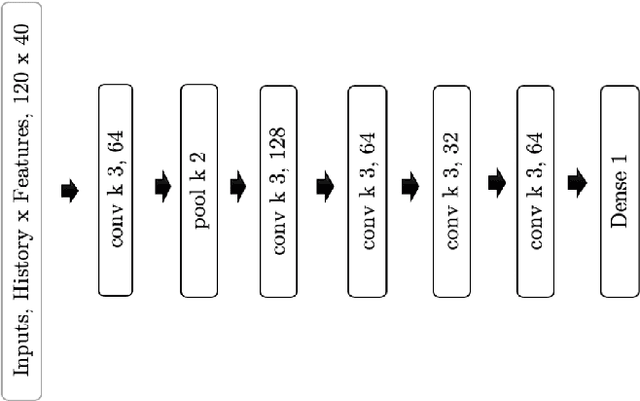
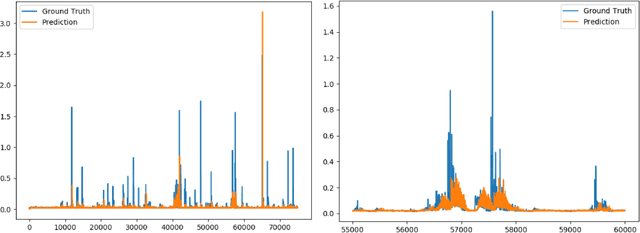
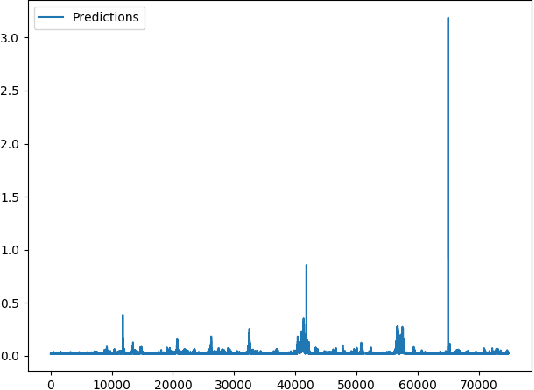
A Global Navigation Satellite System (GNSS) uses a constellation of satellites around the earth for accurate navigation, timing, and positioning. Natural phenomena like space weather introduce irregularities in the Earth's ionosphere, disrupting the propagation of the radio signals that GNSS relies upon. Such disruptions affect both the amplitude and the phase of the propagated waves. No physics-based model currently exists to predict the time and location of these disruptions with sufficient accuracy and at relevant scales. In this paper, we focus on predicting the phase fluctuations of GNSS radio waves, known as phase scintillations. We propose a novel architecture and loss function to predict 1 hour in advance the magnitude of phase scintillations within a time window of plus-minus 5 minutes with state-of-the-art performance.

On the Limitations of Representing Functions on Sets

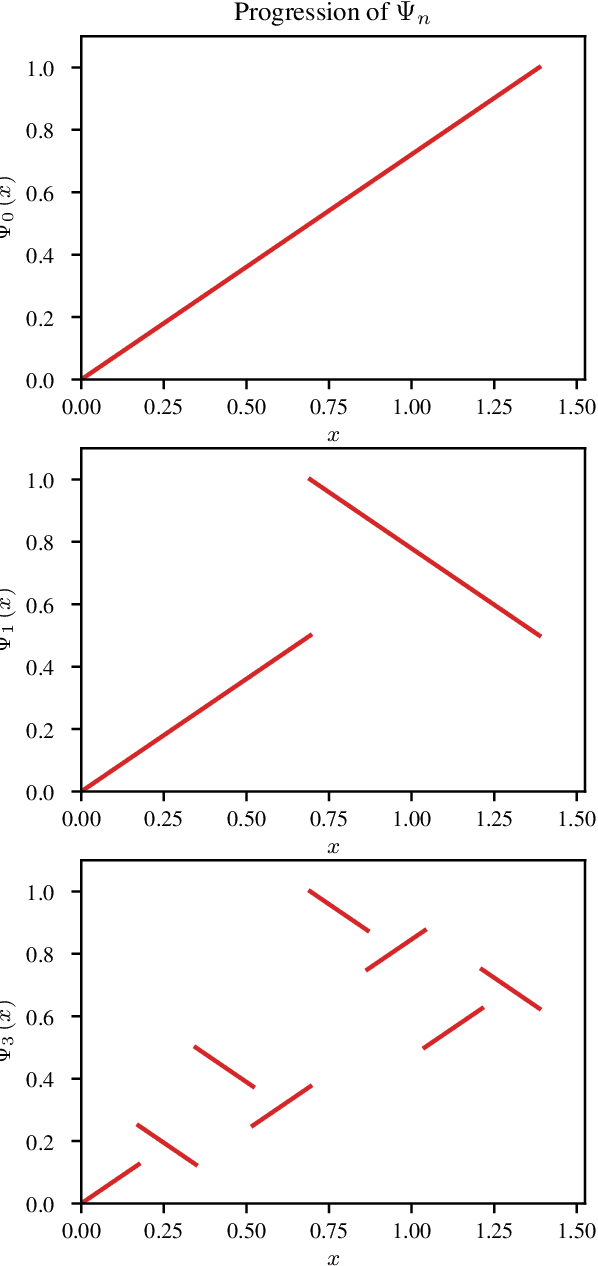
Recent work on the representation of functions on sets has considered the use of summation in a latent space to enforce permutation invariance. In particular, it has been conjectured that the dimension of this latent space may remain fixed as the cardinality of the sets under consideration increases. However, we demonstrate that the analysis leading to this conjecture requires mappings which are highly discontinuous and argue that this is only of limited practical use. Motivated by this observation, we prove that an implementation of this model via continuous mappings (as provided by e.g. neural networks or Gaussian processes) actually imposes a constraint on the dimensionality of the latent space. Practical universal function representation for set inputs can only be achieved with a latent dimension at least the size of the maximum number of input elements.

VBALD - Variational Bayesian Approximation of Log Determinants

Evaluating the log determinant of a positive definite matrix is ubiquitous in machine learning. Applications thereof range from Gaussian processes, minimum-volume ellipsoids, metric learning, kernel learning, Bayesian neural networks, Determinental Point Processes, Markov random fields to partition functions of discrete graphical models. In order to avoid the canonical, yet prohibitive, Cholesky $\mathcal{O}(n^{3})$ computational cost, we propose a novel approach, with complexity $\mathcal{O}(n^{2})$, based on a constrained variational Bayes algorithm. We compare our method to Taylor, Chebyshev and Lanczos approaches and show state of the art performance on both synthetic and real-world datasets.