IDF++: Analyzing and Improving Integer Discrete Flows for Lossless Compression
Paper and Code
Jun 22, 2020
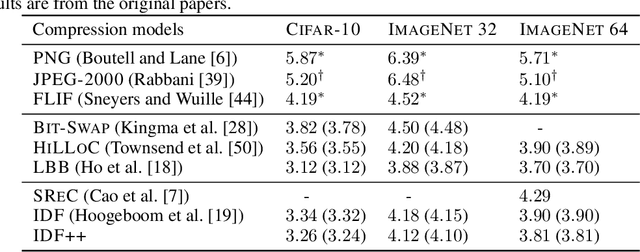


In this paper we analyse and improve integer discrete flows for lossless compression. Integer discrete flows are a recently proposed class of models that learn invertible transformations for integer-valued random variables. Due to its discrete nature, they can be combined in a straightforward manner with entropy coding schemes for lossless compression without the need for bits-back coding. We discuss the potential difference in flexibility between invertible flows for discrete random variables and flows for continuous random variables and show that (integer) discrete flows are more flexible than previously claimed. We furthermore investigate the influence of quantization operators on optimization and gradient bias in integer discrete flows. Finally, we introduce modifications to the architecture to improve the performance of this model class for lossless compression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge