Dev Rajnarayan
Bias-Variance Techniques for Monte Carlo Optimization: Cross-validation for the CE Method
Oct 06, 2008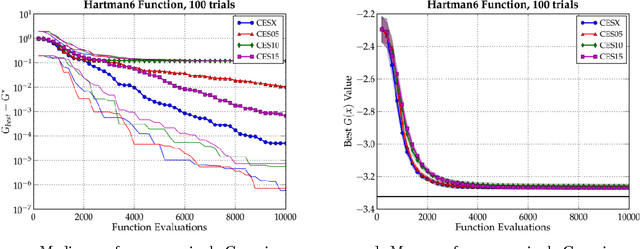
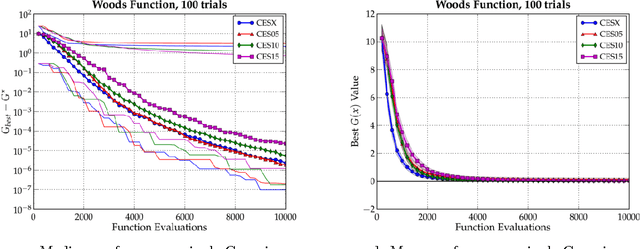
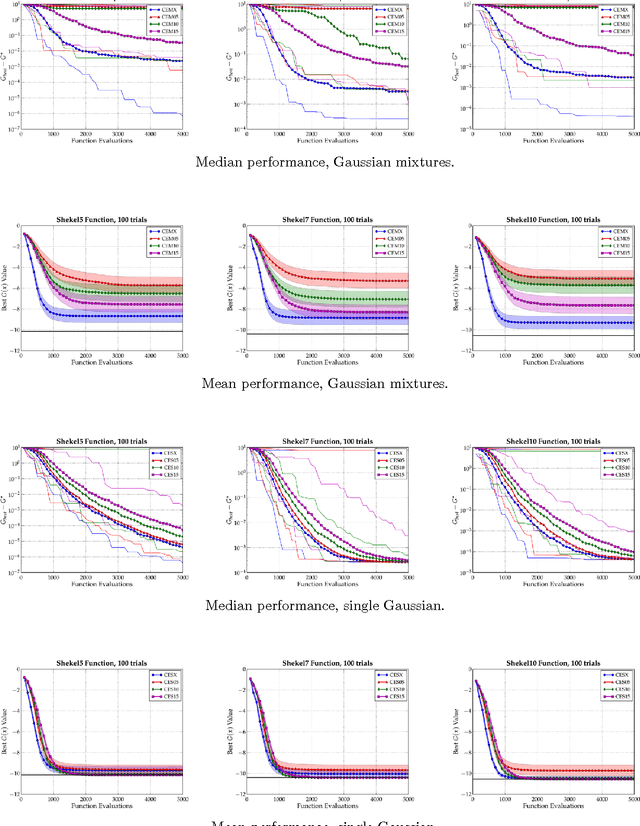
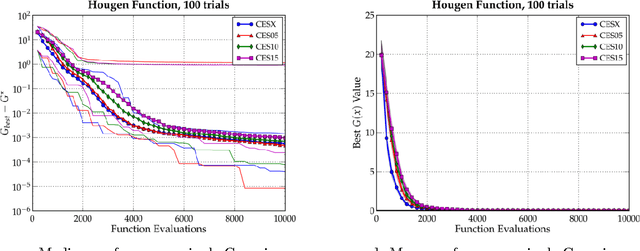
Abstract:In this paper, we examine the CE method in the broad context of Monte Carlo Optimization (MCO) and Parametric Learning (PL), a type of machine learning. A well-known overarching principle used to improve the performance of many PL algorithms is the bias-variance tradeoff. This tradeoff has been used to improve PL algorithms ranging from Monte Carlo estimation of integrals, to linear estimation, to general statistical estimation. Moreover, as described by, MCO is very closely related to PL. Owing to this similarity, the bias-variance tradeoff affects MCO performance, just as it does PL performance. In this article, we exploit the bias-variance tradeoff to enhance the performance of MCO algorithms. We use the technique of cross-validation, a technique based on the bias-variance tradeoff, to significantly improve the performance of the Cross Entropy (CE) method, which is an MCO algorithm. In previous work we have confirmed that other PL techniques improve the perfomance of other MCO algorithms. We conclude that the many techniques pioneered in PL could be investigated as ways to improve MCO algorithms in general, and the CE method in particular.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge