Maxinder S. Kanwal
Comparing Information-Theoretic Measures of Complexity in Boltzmann Machines
Jul 30, 2017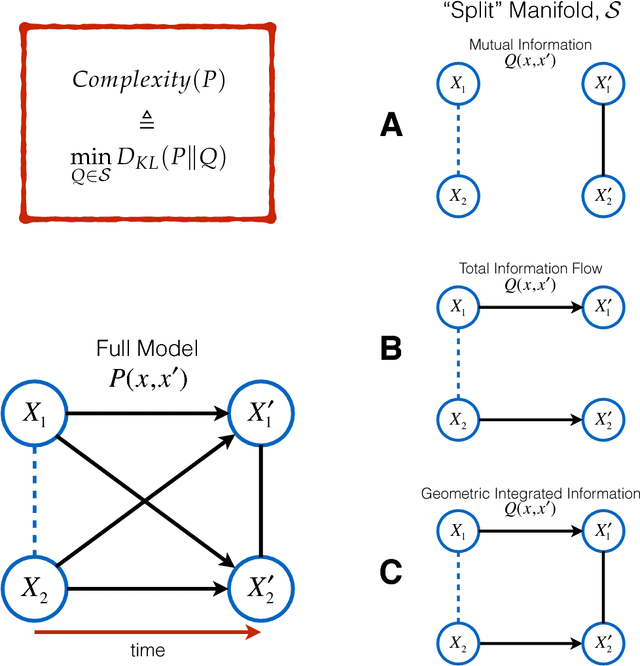
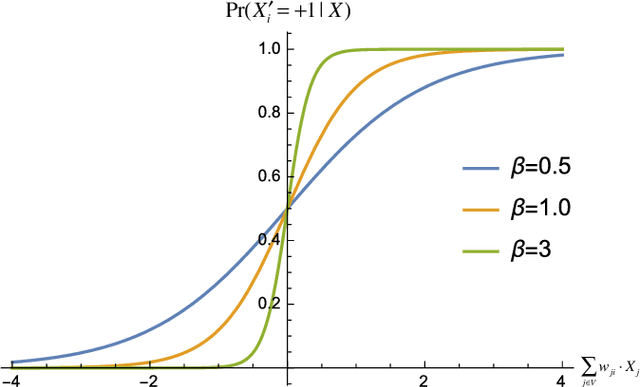
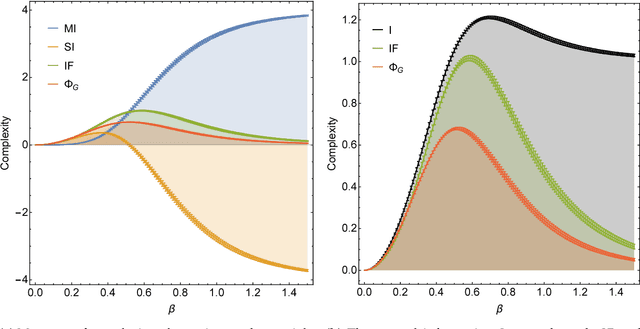
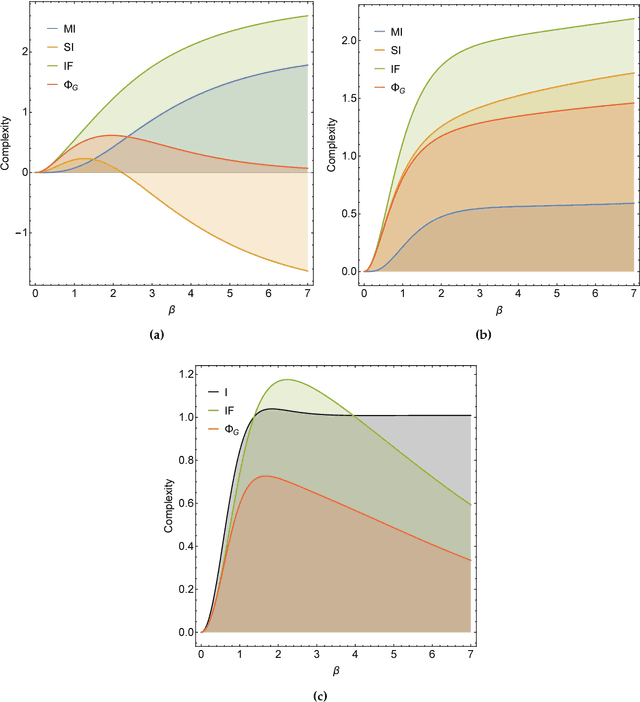
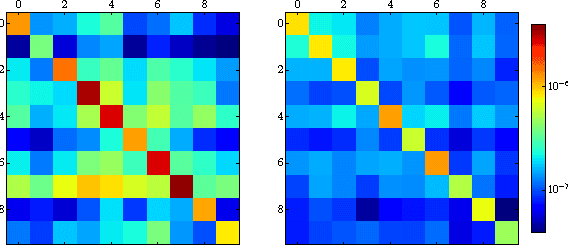
Abstract:In the past three decades, many theoretical measures of complexity have been proposed to help understand complex systems. In this work, for the first time, we place these measures on a level playing field, to explore the qualitative similarities and differences between them, and their shortcomings. Specifically, using the Boltzmann machine architecture (a fully connected recurrent neural network) with uniformly distributed weights as our model of study, we numerically measure how complexity changes as a function of network dynamics and network parameters. We apply an extension of one such information-theoretic measure of complexity to understand incremental Hebbian learning in Hopfield networks, a fully recurrent architecture model of autoassociative memory. In the course of Hebbian learning, the total information flow reflects a natural upward trend in complexity as the network attempts to learn more and more patterns.
* 16 pages, 7 figures; Appears in Entropy, Special Issue "Information Geometry II"
A Closer Look at Memorization in Deep Networks
Jul 01, 2017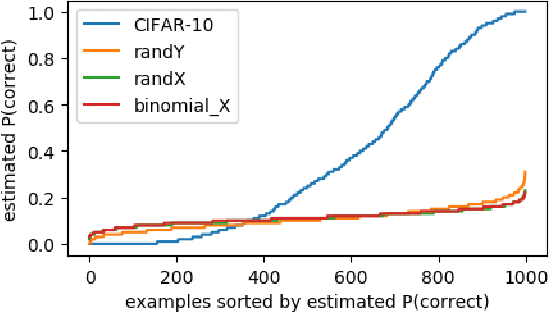

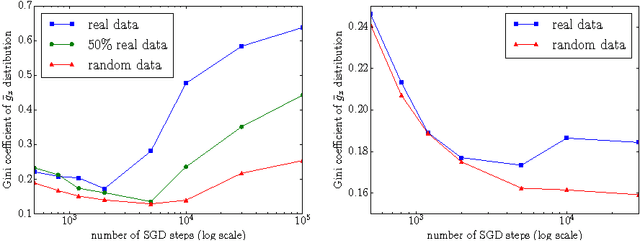
Abstract:We examine the role of memorization in deep learning, drawing connections to capacity, generalization, and adversarial robustness. While deep networks are capable of memorizing noise data, our results suggest that they tend to prioritize learning simple patterns first. In our experiments, we expose qualitative differences in gradient-based optimization of deep neural networks (DNNs) on noise vs. real data. We also demonstrate that for appropriately tuned explicit regularization (e.g., dropout) we can degrade DNN training performance on noise datasets without compromising generalization on real data. Our analysis suggests that the notions of effective capacity which are dataset independent are unlikely to explain the generalization performance of deep networks when trained with gradient based methods because training data itself plays an important role in determining the degree of memorization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge