Hierarchical Models as Marginals of Hierarchical Models
Paper and Code
Mar 07, 2016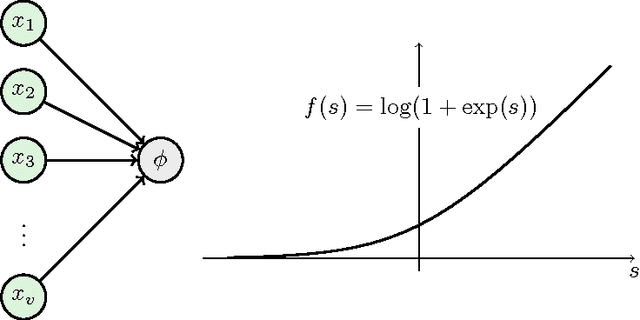
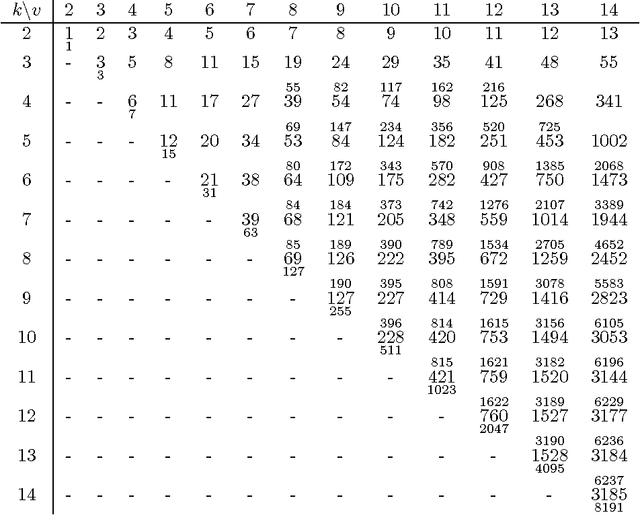
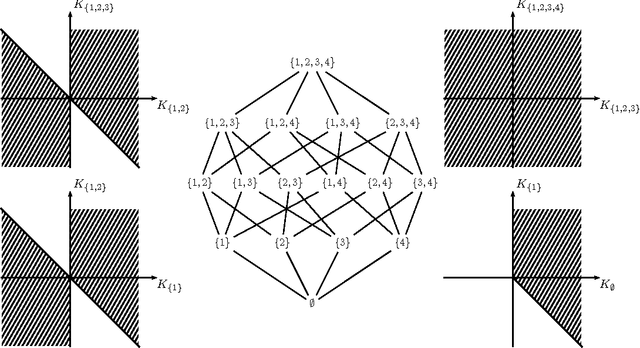
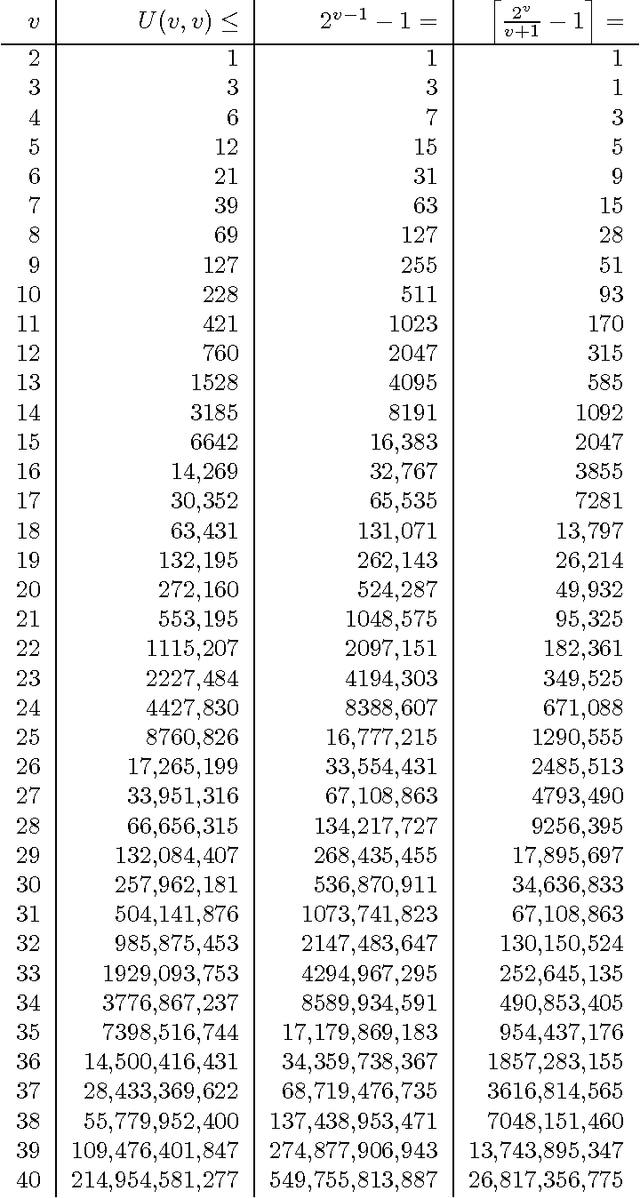
We investigate the representation of hierarchical models in terms of marginals of other hierarchical models with smaller interactions. We focus on binary variables and marginals of pairwise interaction models whose hidden variables are conditionally independent given the visible variables. In this case the problem is equivalent to the representation of linear subspaces of polynomials by feedforward neural networks with soft-plus computational units. We show that every hidden variable can freely model multiple interactions among the visible variables, which allows us to generalize and improve previous results. In particular, we show that a restricted Boltzmann machine with less than $[ 2(\log(v)+1) / (v+1) ] 2^v-1$ hidden binary variables can approximate every distribution of $v$ visible binary variables arbitrarily well, compared to $2^{v-1}-1$ from the best previously known result.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge