Discrete Restricted Boltzmann Machines
Paper and Code
Apr 22, 2014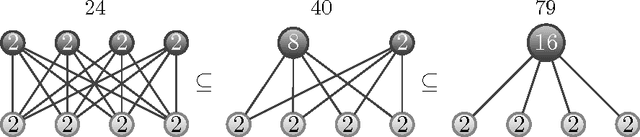

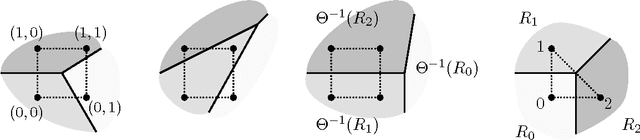
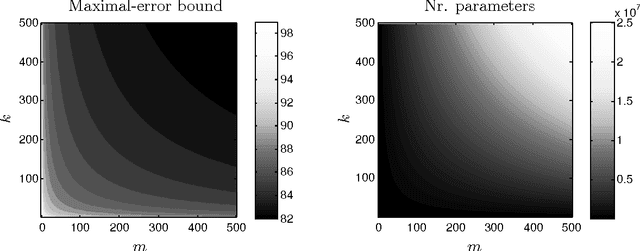
We describe discrete restricted Boltzmann machines: probabilistic graphical models with bipartite interactions between visible and hidden discrete variables. Examples are binary restricted Boltzmann machines and discrete naive Bayes models. We detail the inference functions and distributed representations arising in these models in terms of configurations of projected products of simplices and normal fans of products of simplices. We bound the number of hidden variables, depending on the cardinalities of their state spaces, for which these models can approximate any probability distribution on their visible states to any given accuracy. In addition, we use algebraic methods and coding theory to compute their dimension.
* 18 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge