Fractal Structure and Generalization Properties of Stochastic Optimization Algorithms
Paper and Code
Jun 09, 2021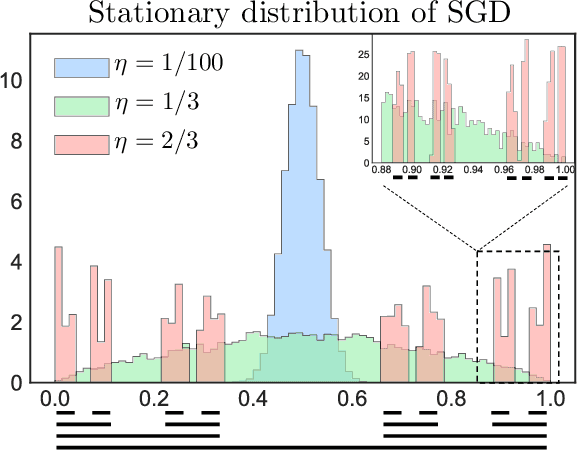
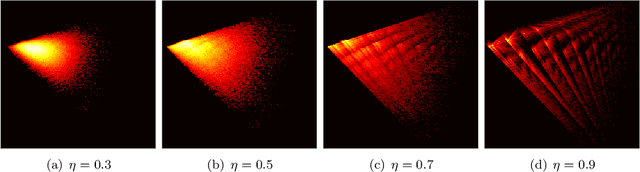
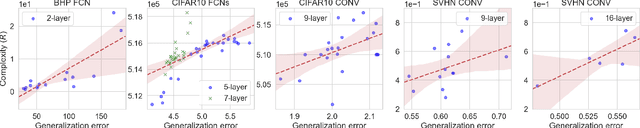
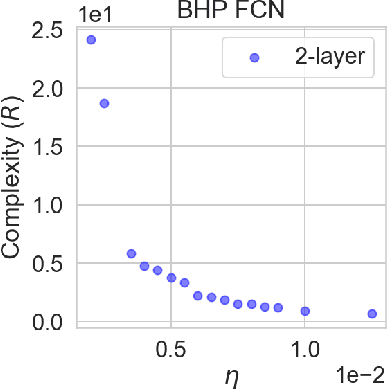
Understanding generalization in deep learning has been one of the major challenges in statistical learning theory over the last decade. While recent work has illustrated that the dataset and the training algorithm must be taken into account in order to obtain meaningful generalization bounds, it is still theoretically not clear which properties of the data and the algorithm determine the generalization performance. In this study, we approach this problem from a dynamical systems theory perspective and represent stochastic optimization algorithms as random iterated function systems (IFS). Well studied in the dynamical systems literature, under mild assumptions, such IFSs can be shown to be ergodic with an invariant measure that is often supported on sets with a fractal structure. As our main contribution, we prove that the generalization error of a stochastic optimization algorithm can be bounded based on the `complexity' of the fractal structure that underlies its invariant measure. Leveraging results from dynamical systems theory, we show that the generalization error can be explicitly linked to the choice of the algorithm (e.g., stochastic gradient descent -- SGD), algorithm hyperparameters (e.g., step-size, batch-size), and the geometry of the problem (e.g., Hessian of the loss). We further specialize our results to specific problems (e.g., linear/logistic regression, one hidden-layered neural networks) and algorithms (e.g., SGD and preconditioned variants), and obtain analytical estimates for our bound.For modern neural networks, we develop an efficient algorithm to compute the developed bound and support our theory with various experiments on neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge