Explicit Regularisation in Gaussian Noise Injections
Paper and Code
Jul 14, 2020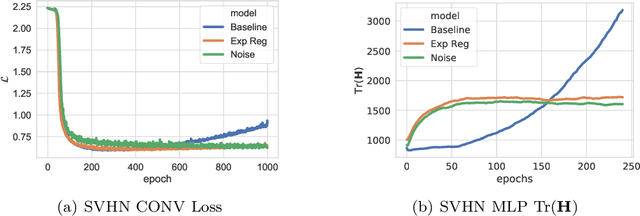
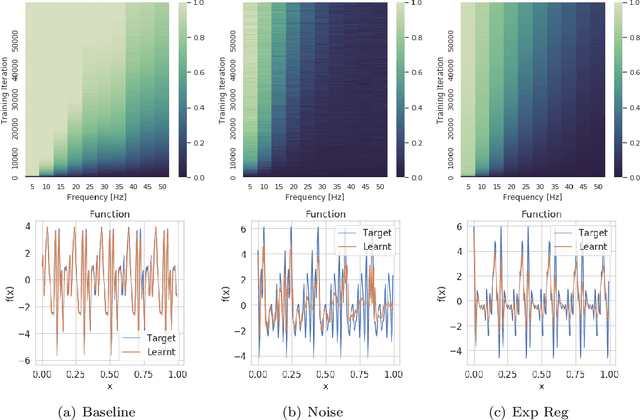
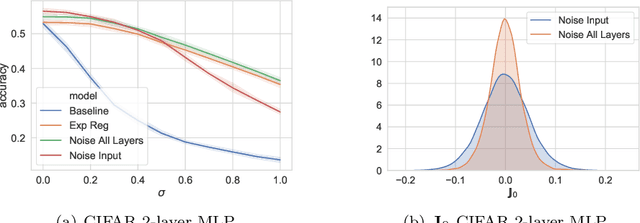
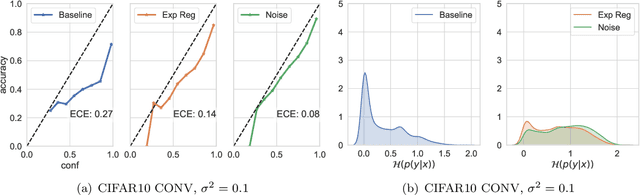
We study the regularisation induced in neural networks by Gaussian noise injections (GNIs). Though such injections have been extensively studied when applied to data, there have been few studies on understanding the regularising effect they induce when applied to network activations. Here we derive the explicit regulariser of GNIs, obtained by marginalising out the injected noise, and show that it is a form of Tikhonov regularisation which penalises functions with high-frequency components in the Fourier domain. We show analytically and empirically that such regularisation produces calibrated classifiers with large classification margins and that the explicit regulariser we derive is able to reproduce these effects.
* 10 Pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge