I Don't Need $\mathbf{u}$: Identifiable Non-Linear ICA Without Side Information

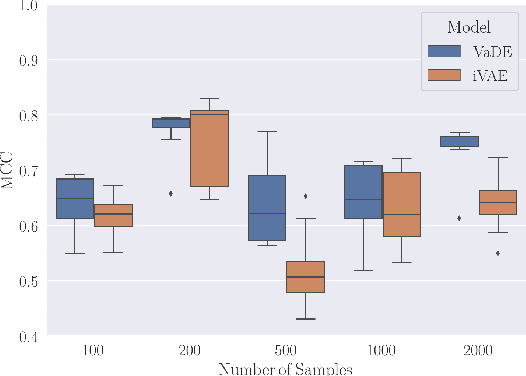
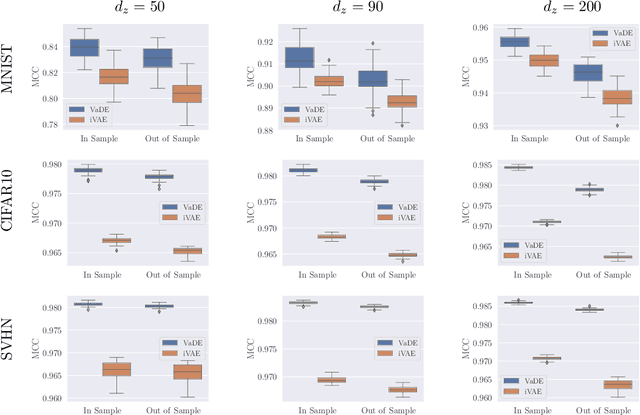
In this work we introduce a new approach for identifiable non-linear ICA models. Recently there has been a renaissance in identifiability results in deep generative models, not least for non-linear ICA. These prior works, however, have assumed access to a sufficiently-informative auxiliary set of observations, denoted $\mathbf{u}$. We show here how identifiability can be obtained in the absence of this side-information, rendering possible fully-unsupervised identifiable non-linear ICA. While previous theoretical results have established the impossibility of identifiable non-linear ICA in the presence of infinitely-flexible universal function approximators, here we rely on the intrinsically-finite modelling capacity of any particular chosen parameterisation of a deep generative model. In particular, we focus on generative models which perform clustering in their latent space -- a model structure which matches previous identifiable models, but with the learnt clustering providing a synthetic form of auxiliary information. We evaluate our proposals using VAEs, on synthetic and image datasets, and find that the learned clusterings function effectively: deep generative models with latent clusterings are empirically identifiable, to the same degree as models which rely on side information.