Evidential time-to-event prediction model with well-calibrated uncertainty estimation
Paper and Code
Nov 12, 2024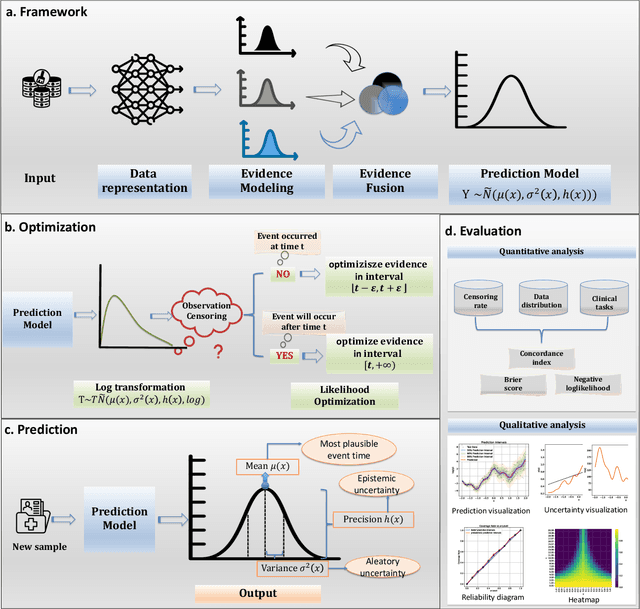

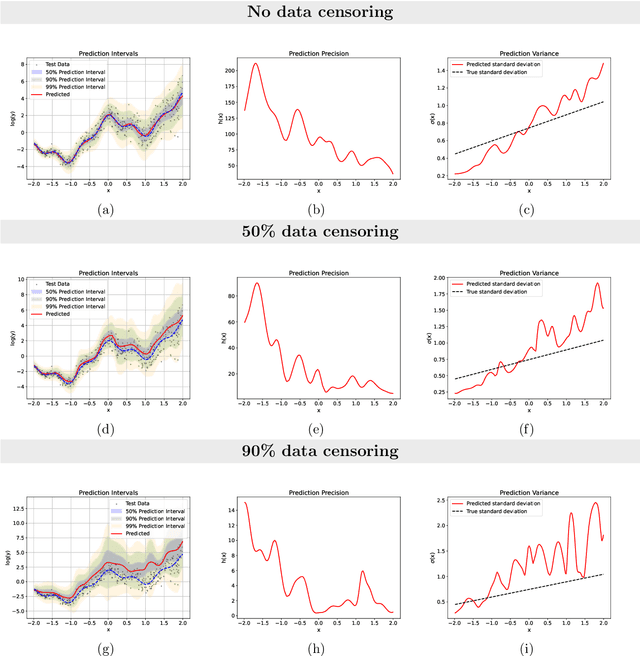
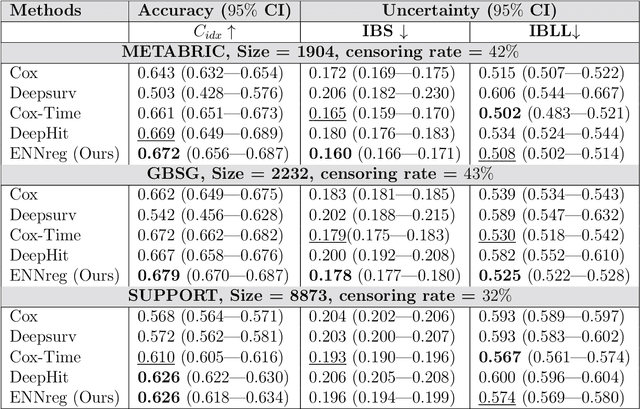
Time-to-event analysis, or Survival analysis, provides valuable insights into clinical prognosis and treatment recommendations. However, this task is typically more challenging than other regression tasks due to the censored observations. Moreover, concerns regarding the reliability of predictions persist among clinicians, mainly attributed to the absence of confidence assessment, robustness, and calibration of prediction. To address those challenges, we introduce an evidential regression model designed especially for time-to-event prediction tasks, with which the most plausible event time, is directly quantified by aggregated Gaussian random fuzzy numbers (GRFNs). The GRFNs are a newly introduced family of random fuzzy subsets of the real line that generalizes both Gaussian random variables and Gaussian possibility distributions. Different from conventional methods that construct models based on strict data distribution, e.g., proportional hazard function, our model only assumes the event time is encoded in a real line GFRN without any strict distribution assumption, therefore offering more flexibility in complex data scenarios. Furthermore, the epistemic and aleatory uncertainty regarding the event time is quantified within the aggregated GRFN as well. Our model can, therefore, provide more detailed clinical decision-making guidance with two more degrees of information. The model is fit by minimizing a generalized negative log-likelihood function that accounts for data censoring based on uncertainty evidence reasoning. Experimental results on simulated datasets with varying data distributions and censoring scenarios, as well as on real-world datasets across diverse clinical settings and tasks, demonstrate that our model achieves both accurate and reliable performance, outperforming state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge