DANCER: Dance ANimation via Condition Enhancement and Rendering with diffusion model

Recently, diffusion models have shown their impressive ability in visual generation tasks. Besides static images, more and more research attentions have been drawn to the generation of realistic videos. The video generation not only has a higher requirement for the quality, but also brings a challenge in ensuring the video continuity. Among all the video generation tasks, human-involved contents, such as human dancing, are even more difficult to generate due to the high degrees of freedom associated with human motions. In this paper, we propose a novel framework, named as DANCER (Dance ANimation via Condition Enhancement and Rendering with Diffusion Model), for realistic single-person dance synthesis based on the most recent stable video diffusion model. As the video generation is generally guided by a reference image and a video sequence, we introduce two important modules into our framework to fully benefit from the two inputs. More specifically, we design an Appearance Enhancement Module (AEM) to focus more on the details of the reference image during the generation, and extend the motion guidance through a Pose Rendering Module (PRM) to capture pose conditions from extra domains. To further improve the generation capability of our model, we also collect a large amount of video data from Internet, and generate a novel datasetTikTok-3K to enhance the model training. The effectiveness of the proposed model has been evaluated through extensive experiments on real-world datasets, where the performance of our model is superior to that of the state-of-the-art methods. All the data and codes will be released upon acceptance.

CodeBrain: Bridging Decoupled Tokenizer and Multi-Scale Architecture for EEG Foundation Model

Electroencephalography (EEG) provides real-time insights into brain activity and is widely used in neuroscience. However, variations in channel configurations, sequence lengths, and task objectives limit the transferability of traditional task-specific models. Although recent EEG foundation models (EFMs) aim to learn generalizable representations, they struggle with limited heterogeneous representation capacity and inefficiency in capturing multi-scale brain dependencies. To address these challenges, we propose CodeBrain, an efficient EFM structurally aligned with brain organization, trained in two stages. (1) We introduce a TFDual-Tokenizer that independently tokenizes heterogeneous temporal and frequency components, enabling a quadratic expansion of the discrete representation space. This also offers a degree of interpretability through cross-domain token analysis. (2) We propose the EEGSSM, which combines a structured global convolution architecture and a sliding window attention mechanism to jointly model sparse long-range and local dependencies. Unlike fully connected Transformer models, EEGSSM better reflects the brain's small-world topology and efficiently captures EEG's inherent multi-scale structure. EEGSSM is trained with a masked self-supervised learning objective to predict token indices obtained in TFDual-Tokenizer. Comprehensive experiments on 10 public EEG datasets demonstrate the generalizability of CodeBrain with linear probing. By offering biologically informed and interpretable EEG modeling, CodeBrain lays the foundation for future neuroscience research. Both code and pretraining weights will be released in the future version.

EsurvFusion: An evidential multimodal survival fusion model based on Gaussian random fuzzy numbers

Multimodal survival analysis aims to combine heterogeneous data sources (e.g., clinical, imaging, text, genomics) to improve the prediction quality of survival outcomes. However, this task is particularly challenging due to high heterogeneity and noise across data sources, which vary in structure, distribution, and context. Additionally, the ground truth is often censored (uncertain) due to incomplete follow-up data. In this paper, we propose a novel evidential multimodal survival fusion model, EsurvFusion, designed to combine multimodal data at the decision level through an evidence-based decision fusion layer that jointly addresses both data and model uncertainty while incorporating modality-level reliability. Specifically, EsurvFusion first models unimodal data with newly introduced Gaussian random fuzzy numbers, producing unimodal survival predictions along with corresponding aleatoric and epistemic uncertainties. It then estimates modality-level reliability through a reliability discounting layer to correct the misleading impact of noisy data modalities. Finally, a multimodal evidence-based fusion layer is introduced to combine the discounted predictions to form a unified, interpretable multimodal survival analysis model, revealing each modality's influence based on the learned reliability coefficients. This is the first work that studies multimodal survival analysis with both uncertainty and reliability. Extensive experiments on four multimodal survival datasets demonstrate the effectiveness of our model in handling high heterogeneity data, establishing new state-of-the-art on several benchmarks.

Adaptively Controllable Diffusion Model for Efficient Conditional Image Generation

With the development of artificial intelligence, more and more attention has been put onto generative models, which represent the creativity, a very important aspect of intelligence. In recent years, diffusion models have been studied and proven to be more reasonable and effective than previous methods. However, common diffusion frameworks suffer from controllability problems. Although extra conditions have been considered by some work to guide the diffusion process for a specific target generation, it only controls the generation result but not its process. In this work, we propose a new adaptive framework, $\textit{Adaptively Controllable Diffusion (AC-Diff) Model}$, to automatically and fully control the generation process, including not only the type of generation result but also the length and parameters of the generation process. Both inputs and conditions will be first fed into a $\textit{Conditional Time-Step (CTS) Module}$ to determine the number of steps needed for a generation. Then according to the length of the process, the diffusion rate parameters will be estimated through our $\textit{Adaptive Hybrid Noise Schedule (AHNS) Module}$. We further train the network with the corresponding adaptive sampling mechanism to learn how to adjust itself according to the conditions for the overall performance improvement. To enable its practical applications, AC-Diff is expected to largely reduce the average number of generation steps and execution time while maintaining the same performance as done in the literature diffusion models.

Puppet-CNN: Input-Adaptive Convolutional Neural Networks with Model Compression using Ordinary Differential Equation

Convolutional Neural Network (CNN) has been applied to more and more scenarios due to its excellent performance in many machine learning tasks, especially with deep and complex structures. However, as the network goes deeper, more parameters need to be stored and optimized. Besides, almost all common CNN models adopt "train-and-use" strategy where the structure is pre-defined and the kernel parameters are fixed after the training with the same structure and set of parameters used for all data without considering the content complexity. In this paper, we propose a new CNN framework, named as $\textit{Puppet-CNN}$, which contains two modules: a $\textit{puppet module}$ and a $\textit{puppeteer module}$. The puppet module is a CNN model used to actually process the input data just like other works, but its depth and kernels are generated by the puppeteer module (realized with Ordinary Differential Equation (ODE)) based on the input complexity each time. By recurrently generating kernel parameters in the puppet module, we can take advantage of the dependence among kernels of different convolutional layers to significantly reduce the size of CNN model by only storing and training the parameters of the much smaller puppeteer ODE module. Through experiments on several datasets, our method has proven to be superior than the traditional CNNs on both performance and efficiency. The model size can be reduced more than 10 times.

Map-Free Trajectory Prediction with Map Distillation and Hierarchical Encoding

Reliable motion forecasting of surrounding agents is essential for ensuring the safe operation of autonomous vehicles. Many existing trajectory prediction methods rely heavily on high-definition (HD) maps as strong driving priors. However, the availability and accuracy of these priors are not guaranteed due to substantial costs to build, localization errors of vehicles, or ongoing road constructions. In this paper, we introduce MFTP, a Map-Free Trajectory Prediction method that offers several advantages. First, it eliminates the need for HD maps during inference while still benefiting from map priors during training via knowledge distillation. Second, we present a novel hierarchical encoder that effectively extracts spatial-temporal agent features and aggregates them into multiple trajectory queries. Additionally, we introduce an iterative decoder that sequentially decodes trajectory queries to generate the final predictions. Extensive experiments show that our approach achieves state-of-the-art performance on the Argoverse dataset under the map-free setting.

Evidential time-to-event prediction model with well-calibrated uncertainty estimation

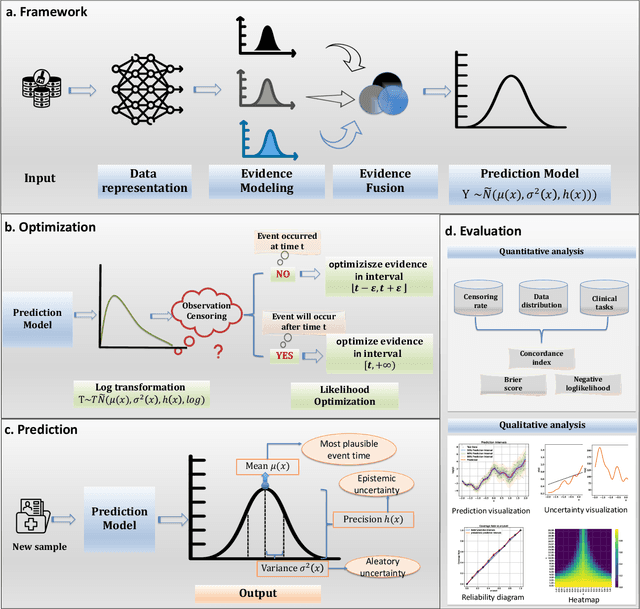
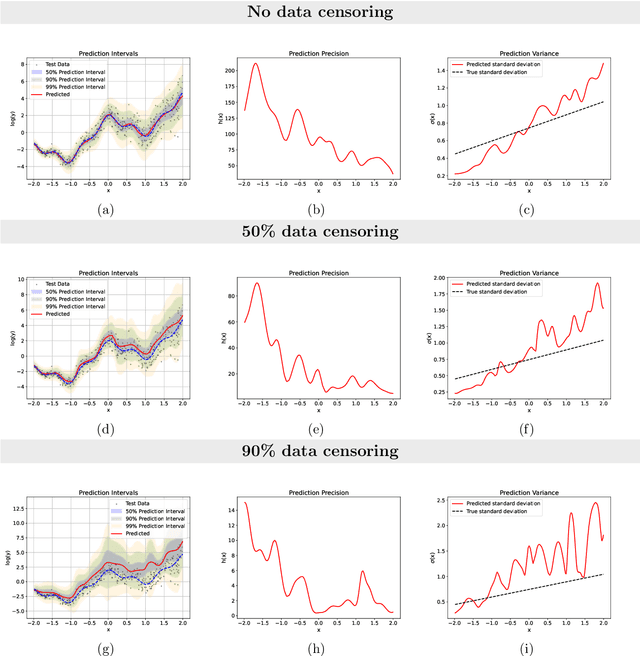
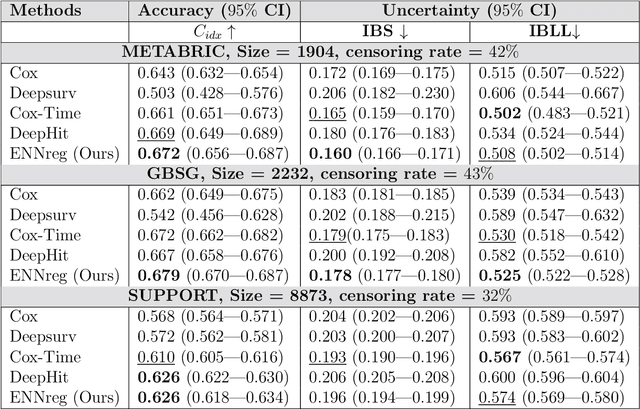
Time-to-event analysis, or Survival analysis, provides valuable insights into clinical prognosis and treatment recommendations. However, this task is typically more challenging than other regression tasks due to the censored observations. Moreover, concerns regarding the reliability of predictions persist among clinicians, mainly attributed to the absence of confidence assessment, robustness, and calibration of prediction. To address those challenges, we introduce an evidential regression model designed especially for time-to-event prediction tasks, with which the most plausible event time, is directly quantified by aggregated Gaussian random fuzzy numbers (GRFNs). The GRFNs are a newly introduced family of random fuzzy subsets of the real line that generalizes both Gaussian random variables and Gaussian possibility distributions. Different from conventional methods that construct models based on strict data distribution, e.g., proportional hazard function, our model only assumes the event time is encoded in a real line GFRN without any strict distribution assumption, therefore offering more flexibility in complex data scenarios. Furthermore, the epistemic and aleatory uncertainty regarding the event time is quantified within the aggregated GRFN as well. Our model can, therefore, provide more detailed clinical decision-making guidance with two more degrees of information. The model is fit by minimizing a generalized negative log-likelihood function that accounts for data censoring based on uncertainty evidence reasoning. Experimental results on simulated datasets with varying data distributions and censoring scenarios, as well as on real-world datasets across diverse clinical settings and tasks, demonstrate that our model achieves both accurate and reliable performance, outperforming state-of-the-art methods.

An evidential time-to-event prediction model based on Gaussian random fuzzy numbers

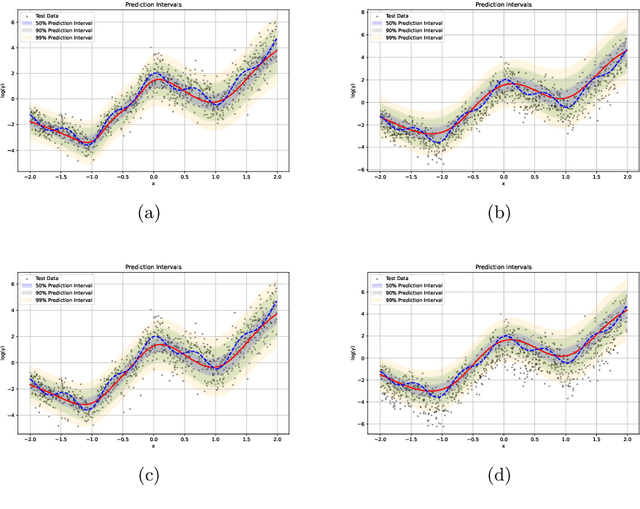
We introduce an evidential model for time-to-event prediction with censored data. In this model, uncertainty on event time is quantified by Gaussian random fuzzy numbers, a newly introduced family of random fuzzy subsets of the real line with associated belief functions, generalizing both Gaussian random variables and Gaussian possibility distributions. Our approach makes minimal assumptions about the underlying time-to-event distribution. The model is fit by minimizing a generalized negative log-likelihood function that accounts for both normal and censored data. Comparative experiments on two real-world datasets demonstrate the very good performance of our model as compared to the state-of-the-art.

A review of uncertainty quantification in medical image analysis: probabilistic and non-probabilistic methods

The comprehensive integration of machine learning healthcare models within clinical practice remains suboptimal, notwithstanding the proliferation of high-performing solutions reported in the literature. A predominant factor hindering widespread adoption pertains to an insufficiency of evidence affirming the reliability of the aforementioned models. Recently, uncertainty quantification methods have been proposed as a potential solution to quantify the reliability of machine learning models and thus increase the interpretability and acceptability of the result. In this review, we offer a comprehensive overview of prevailing methods proposed to quantify uncertainty inherent in machine learning models developed for various medical image tasks. Contrary to earlier reviews that exclusively focused on probabilistic methods, this review also explores non-probabilistic approaches, thereby furnishing a more holistic survey of research pertaining to uncertainty quantification for machine learning models. Analysis of medical images with the summary and discussion on medical applications and the corresponding uncertainty evaluation protocols are presented, which focus on the specific challenges of uncertainty in medical image analysis. We also highlight some potential future research work at the end. Generally, this review aims to allow researchers from both clinical and technical backgrounds to gain a quick and yet in-depth understanding of the research in uncertainty quantification for medical image analysis machine learning models.

Learning Continuous-Time Dynamics by Stochastic Differential Networks

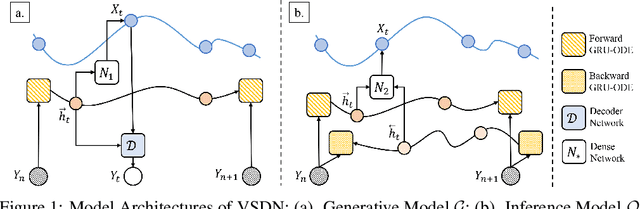
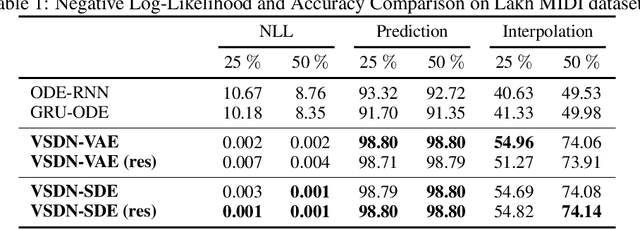
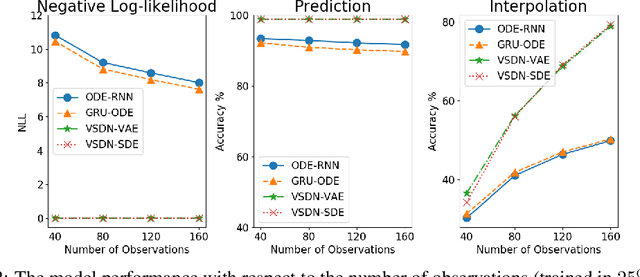
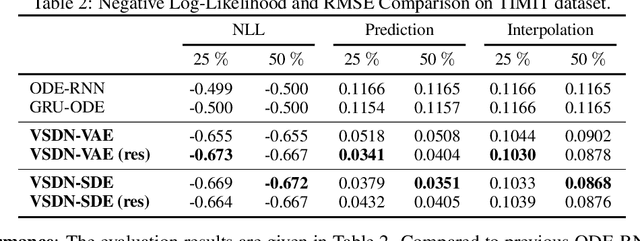
Learning continuous-time stochastic dynamics from sparse or irregular observations is a fundamental and essential problem for many real-world applications. However, for a given system whose latent states and observed data are high-dimensional, it is generally impossible to derive a precise continuous-time stochastic process to describe the system behaviors. To solve the above problem, we apply Variational Bayesian method and propose a flexible continuous-time framework named Variational Stochastic Differential Networks (VSDN), which can model high-dimensional nonlinear stochastic dynamics by deep neural networks. VSDN introduces latent states to modulate the estimated distribution and defines two practical methods to model the stochastic dependency between observations and the states. The first variant, which is called VSDN-VAE, incorporates sequential Variational Auto-Encoder (VAE) to efficiently model the distribution of the latent states. The second variant, called VSDN-SDE, further extends the model capacity of VSDN-VAE by learning a set of Stochastic Differential Equations (SDEs) to fully describe the state transitions. Through comprehensive experiments on symbolic MIDI and speech datasets, we show that VSDNs can accurately model the continuous-time dynamics and achieve remarkable performance on challenging tasks, including online prediction and sequence interpolation.