Learning Continuous-Time Dynamics by Stochastic Differential Networks

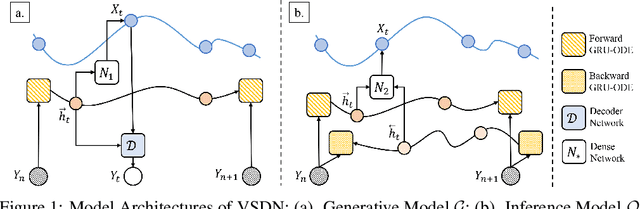
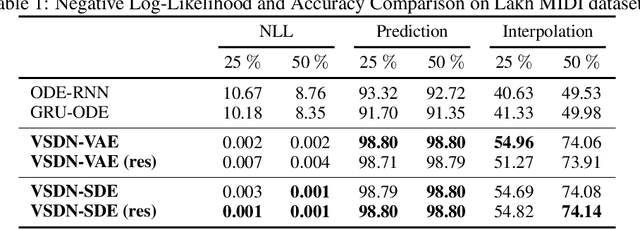
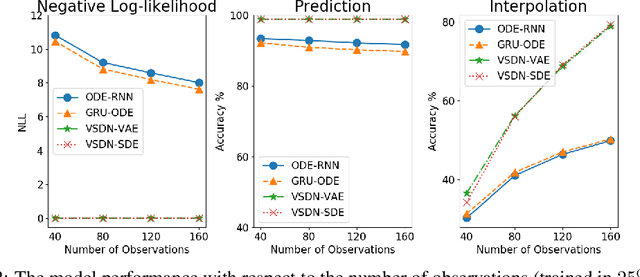
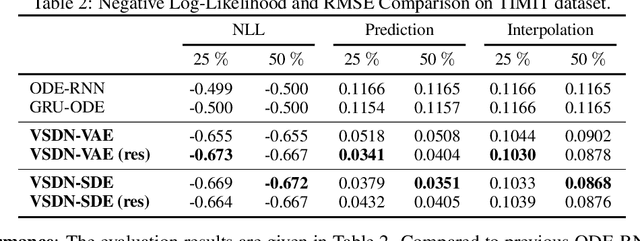
Learning continuous-time stochastic dynamics from sparse or irregular observations is a fundamental and essential problem for many real-world applications. However, for a given system whose latent states and observed data are high-dimensional, it is generally impossible to derive a precise continuous-time stochastic process to describe the system behaviors. To solve the above problem, we apply Variational Bayesian method and propose a flexible continuous-time framework named Variational Stochastic Differential Networks (VSDN), which can model high-dimensional nonlinear stochastic dynamics by deep neural networks. VSDN introduces latent states to modulate the estimated distribution and defines two practical methods to model the stochastic dependency between observations and the states. The first variant, which is called VSDN-VAE, incorporates sequential Variational Auto-Encoder (VAE) to efficiently model the distribution of the latent states. The second variant, called VSDN-SDE, further extends the model capacity of VSDN-VAE by learning a set of Stochastic Differential Equations (SDEs) to fully describe the state transitions. Through comprehensive experiments on symbolic MIDI and speech datasets, we show that VSDNs can accurately model the continuous-time dynamics and achieve remarkable performance on challenging tasks, including online prediction and sequence interpolation.