Evidential time-to-event prediction model with well-calibrated uncertainty estimation

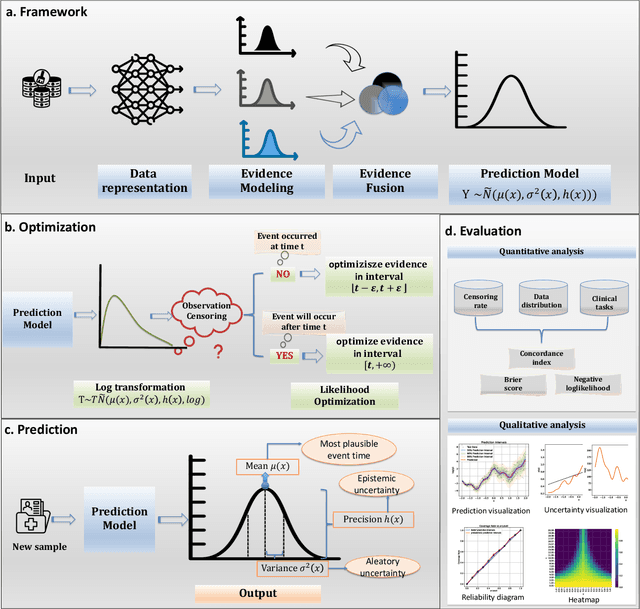
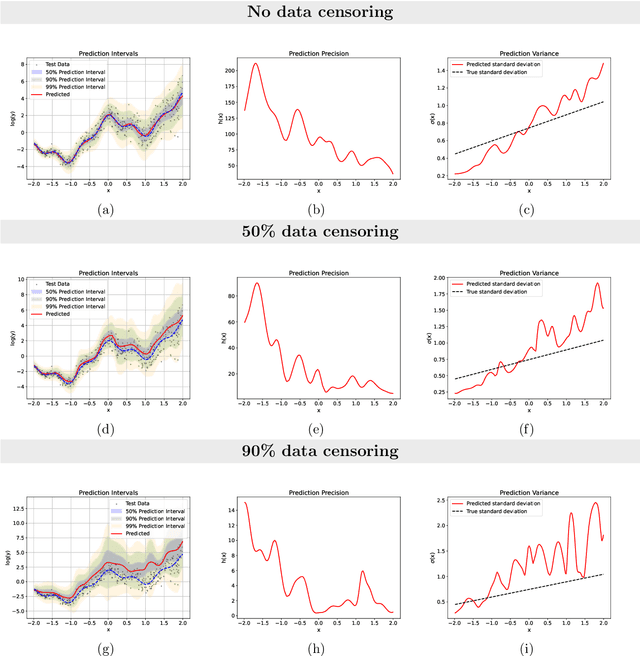
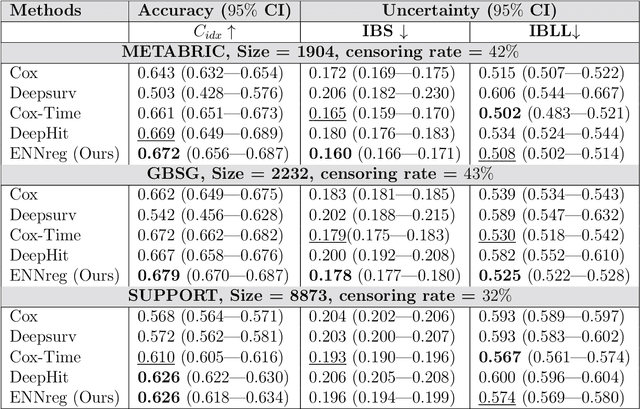
Time-to-event analysis, or Survival analysis, provides valuable insights into clinical prognosis and treatment recommendations. However, this task is typically more challenging than other regression tasks due to the censored observations. Moreover, concerns regarding the reliability of predictions persist among clinicians, mainly attributed to the absence of confidence assessment, robustness, and calibration of prediction. To address those challenges, we introduce an evidential regression model designed especially for time-to-event prediction tasks, with which the most plausible event time, is directly quantified by aggregated Gaussian random fuzzy numbers (GRFNs). The GRFNs are a newly introduced family of random fuzzy subsets of the real line that generalizes both Gaussian random variables and Gaussian possibility distributions. Different from conventional methods that construct models based on strict data distribution, e.g., proportional hazard function, our model only assumes the event time is encoded in a real line GFRN without any strict distribution assumption, therefore offering more flexibility in complex data scenarios. Furthermore, the epistemic and aleatory uncertainty regarding the event time is quantified within the aggregated GRFN as well. Our model can, therefore, provide more detailed clinical decision-making guidance with two more degrees of information. The model is fit by minimizing a generalized negative log-likelihood function that accounts for data censoring based on uncertainty evidence reasoning. Experimental results on simulated datasets with varying data distributions and censoring scenarios, as well as on real-world datasets across diverse clinical settings and tasks, demonstrate that our model achieves both accurate and reliable performance, outperforming state-of-the-art methods.

An evidential time-to-event prediction model based on Gaussian random fuzzy numbers

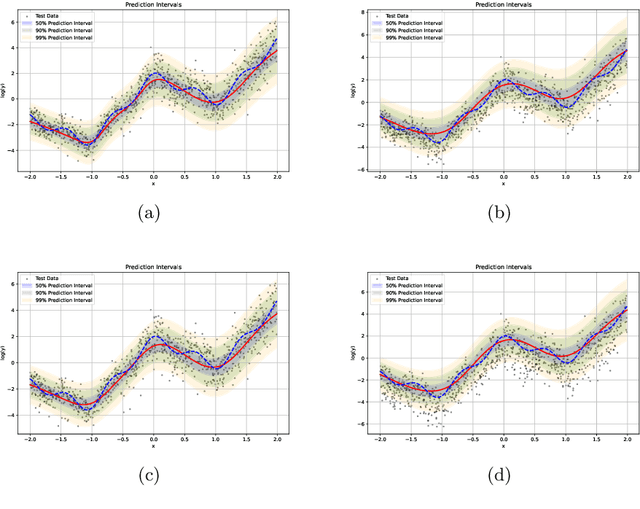
We introduce an evidential model for time-to-event prediction with censored data. In this model, uncertainty on event time is quantified by Gaussian random fuzzy numbers, a newly introduced family of random fuzzy subsets of the real line with associated belief functions, generalizing both Gaussian random variables and Gaussian possibility distributions. Our approach makes minimal assumptions about the underlying time-to-event distribution. The model is fit by minimizing a generalized negative log-likelihood function that accounts for both normal and censored data. Comparative experiments on two real-world datasets demonstrate the very good performance of our model as compared to the state-of-the-art.

Deep evidential fusion with uncertainty quantification and contextual discounting for multimodal medical image segmentation

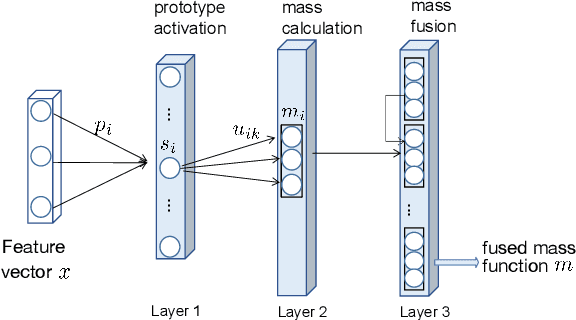
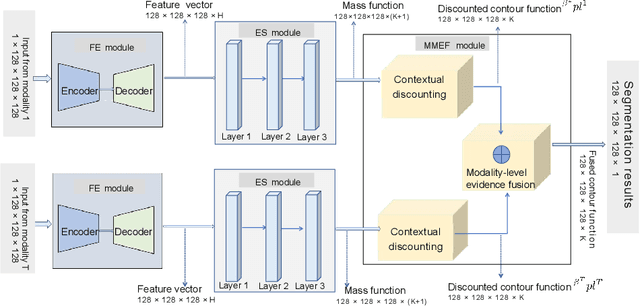
Single-modality medical images generally do not contain enough information to reach an accurate and reliable diagnosis. For this reason, physicians generally diagnose diseases based on multimodal medical images such as, e.g., PET/CT. The effective fusion of multimodal information is essential to reach a reliable decision and explain how the decision is made as well. In this paper, we propose a fusion framework for multimodal medical image segmentation based on deep learning and the Dempster-Shafer theory of evidence. In this framework, the reliability of each single modality image when segmenting different objects is taken into account by a contextual discounting operation. The discounted pieces of evidence from each modality are then combined by Dempster's rule to reach a final decision. Experimental results with a PET-CT dataset with lymphomas and a multi-MRI dataset with brain tumors show that our method outperforms the state-of-the-art methods in accuracy and reliability.

An Evidential Neural Network Model for Regression Based on Random Fuzzy Numbers

We introduce a distance-based neural network model for regression, in which prediction uncertainty is quantified by a belief function on the real line. The model interprets the distances of the input vector to prototypes as pieces of evidence represented by Gaussian random fuzzy numbers (GRFN's) and combined by the generalized product intersection rule, an operator that extends Dempster's rule to random fuzzy sets. The network output is a GRFN that can be summarized by three numbers characterizing the most plausible predicted value, variability around this value, and epistemic uncertainty. Experiments with real datasets demonstrate the very good performance of the method as compared to state-of-the-art evidential and statistical learning algorithms. \keywords{Evidence theory, Dempster-Shafer theory, belief functions, machine learning, random fuzzy sets.

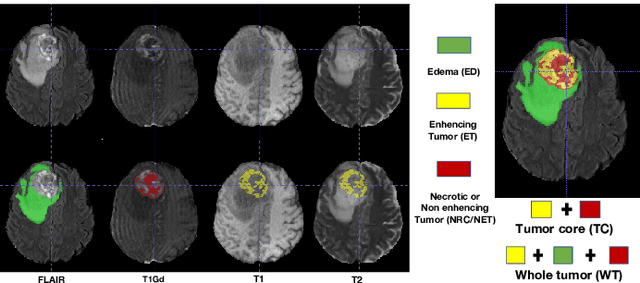
Evidence fusion with contextual discounting for multi-modality medical image segmentation

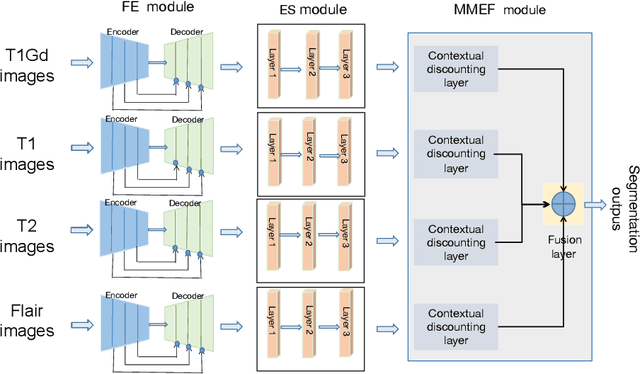
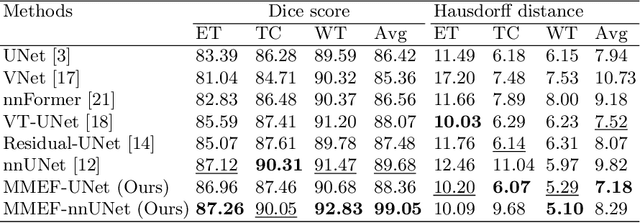
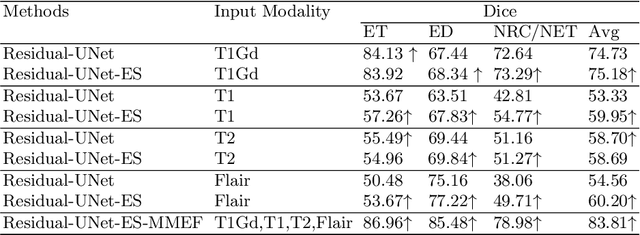
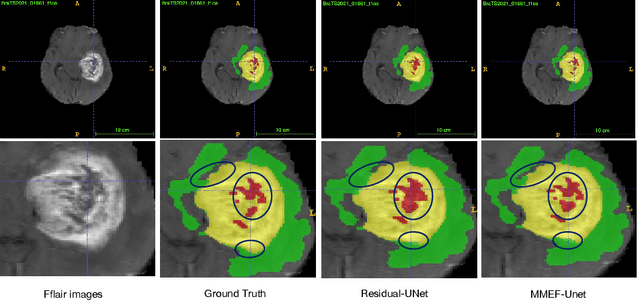
As information sources are usually imperfect, it is necessary to take into account their reliability in multi-source information fusion tasks. In this paper, we propose a new deep framework allowing us to merge multi-MR image segmentation results using the formalism of Dempster-Shafer theory while taking into account the reliability of different modalities relative to different classes. The framework is composed of an encoder-decoder feature extraction module, an evidential segmentation module that computes a belief function at each voxel for each modality, and a multi-modality evidence fusion module, which assigns a vector of discount rates to each modality evidence and combines the discounted evidence using Dempster's rule. The whole framework is trained by minimizing a new loss function based on a discounted Dice index to increase segmentation accuracy and reliability. The method was evaluated on the BraTs 2021 database of 1251 patients with brain tumors. Quantitative and qualitative results show that our method outperforms the state of the art, and implements an effective new idea for merging multi-information within deep neural networks.

Reasoning with fuzzy and uncertain evidence using epistemic random fuzzy sets: general framework and practical models

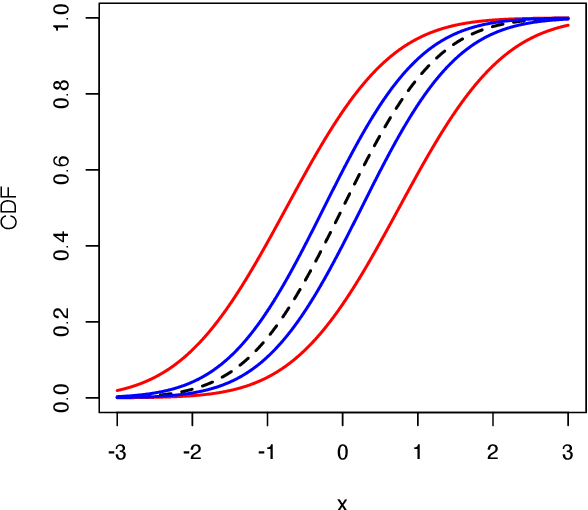
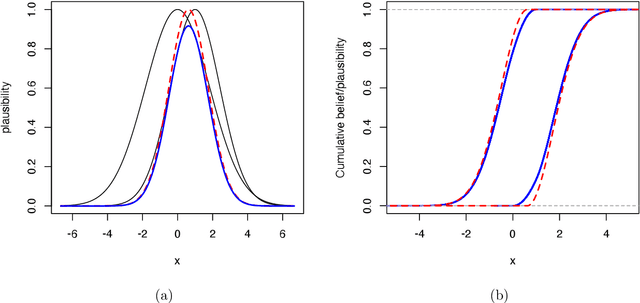
We introduce a general theory of epistemic random fuzzy sets for reasoning with fuzzy or crisp evidence. This framework generalizes both the Dempster-Shafer theory of belief functions, and possibility theory. Independent epistemic random fuzzy sets are combined by the generalized product-intersection rule, which extends both Dempster's rule for combining belief functions, and the product conjunctive combination of possibility distributions. We introduce Gaussian random fuzzy numbers and their multi-dimensional extensions, Gaussian random fuzzy vectors, as practical models for quantifying uncertainty about scalar or vector quantities. Closed-form expressions for the combination, projection and vacuous extension of Gaussian random fuzzy numbers and vectors are derived.

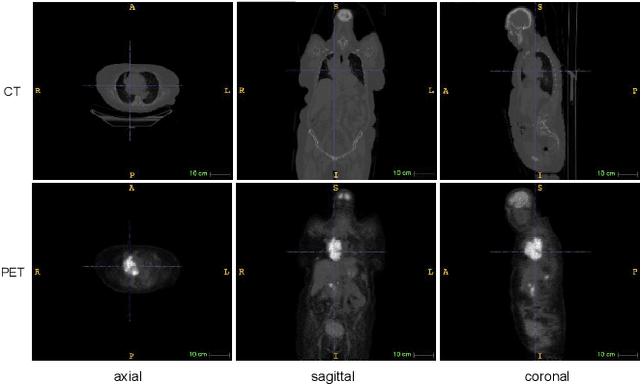
Lymphoma segmentation from 3D PET-CT images using a deep evidential network

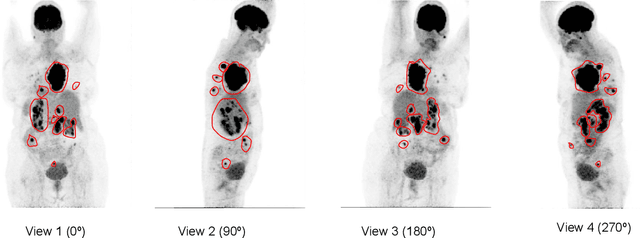
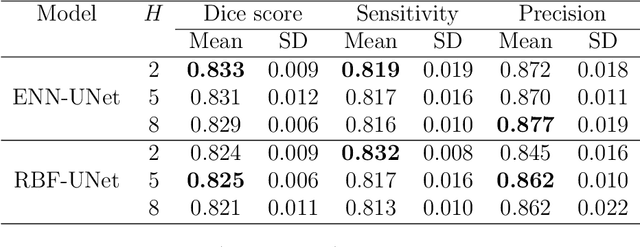
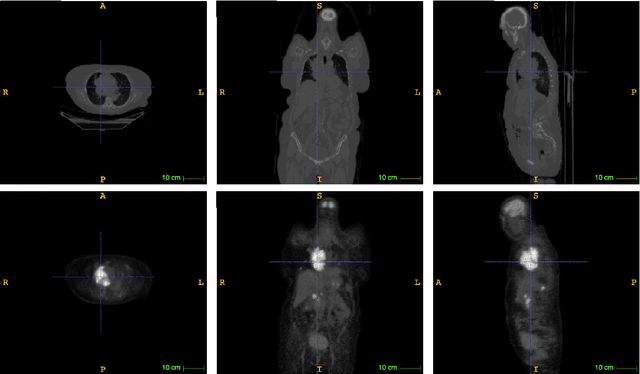
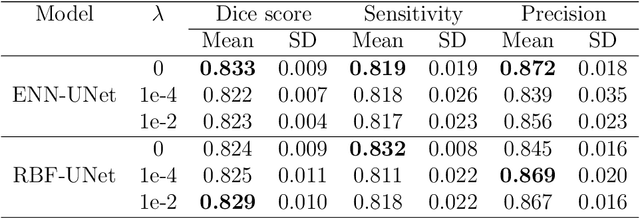
An automatic evidential segmentation method based on Dempster-Shafer theory and deep learning is proposed to segment lymphomas from three-dimensional Positron Emission Tomography (PET) and Computed Tomography (CT) images. The architecture is composed of a deep feature-extraction module and an evidential layer. The feature extraction module uses an encoder-decoder framework to extract semantic feature vectors from 3D inputs. The evidential layer then uses prototypes in the feature space to compute a belief function at each voxel quantifying the uncertainty about the presence or absence of a lymphoma at this location. Two evidential layers are compared, based on different ways of using distances to prototypes for computing mass functions. The whole model is trained end-to-end by minimizing the Dice loss function. The proposed combination of deep feature extraction and evidential segmentation is shown to outperform the baseline UNet model as well as three other state-of-the-art models on a dataset of 173 patients.

Fusion of evidential CNN classifiers for image classification

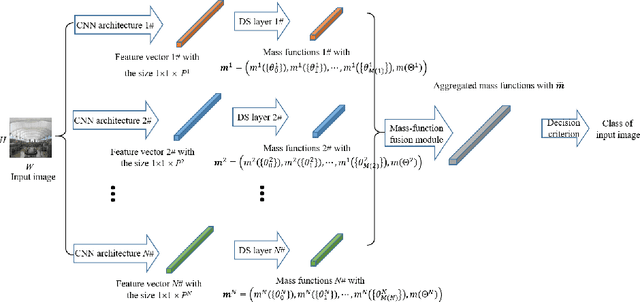
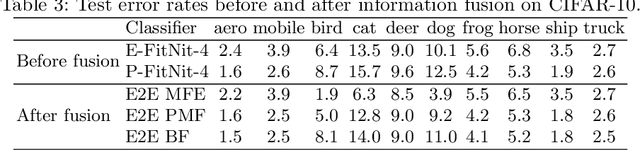
We propose an information-fusion approach based on belief functions to combine convolutional neural networks. In this approach, several pre-trained DS-based CNN architectures extract features from input images and convert them into mass functions on different frames of discernment. A fusion module then aggregates these mass functions using Dempster's rule. An end-to-end learning procedure allows us to fine-tune the overall architecture using a learning set with soft labels, which further improves the classification performance. The effectiveness of this approach is demonstrated experimentally using three benchmark databases.

Deep PET/CT fusion with Dempster-Shafer theory for lymphoma segmentation

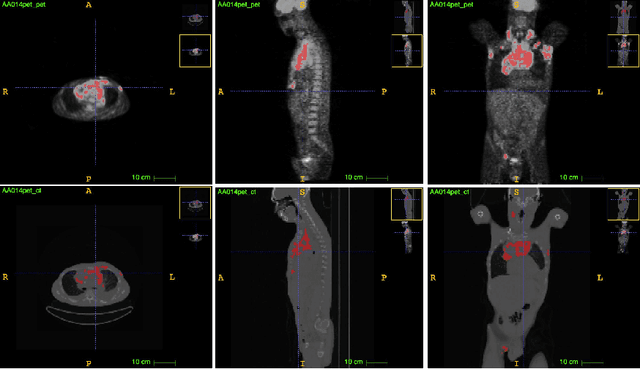
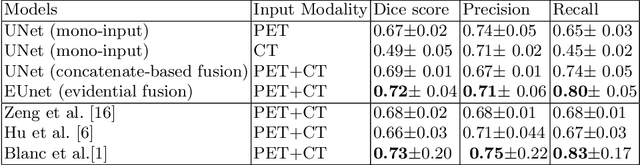
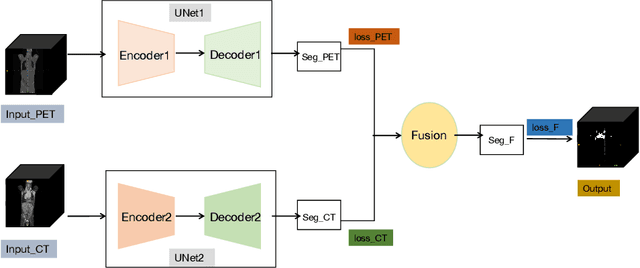
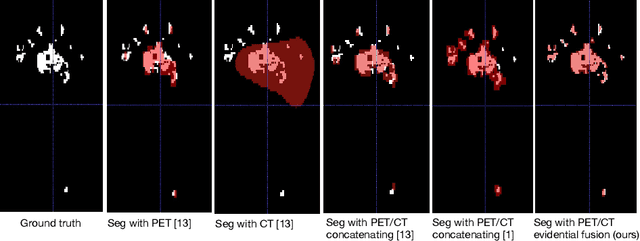
Lymphoma detection and segmentation from whole-body Positron Emission Tomography/Computed Tomography (PET/CT) volumes are crucial for surgical indication and radiotherapy. Designing automatic segmentation methods capable of effectively exploiting the information from PET and CT as well as resolving their uncertainty remain a challenge. In this paper, we propose an lymphoma segmentation model using an UNet with an evidential PET/CT fusion layer. Single-modality volumes are trained separately to get initial segmentation maps and an evidential fusion layer is proposed to fuse the two pieces of evidence using Dempster-Shafer theory (DST). Moreover, a multi-task loss function is proposed: in addition to the use of the Dice loss for PET and CT segmentation, a loss function based on the concordance between the two segmentation is added to constrain the final segmentation. We evaluate our proposal on a database of polycentric PET/CT volumes of patients treated for lymphoma, delineated by the experts. Our method get accurate segmentation results with Dice score of 0.726, without any user interaction. Quantitative results show that our method is superior to the state-of-the-art methods.

Evidential segmentation of 3D PET/CT images

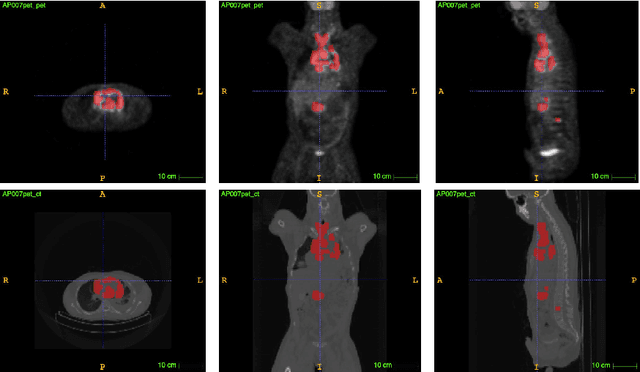
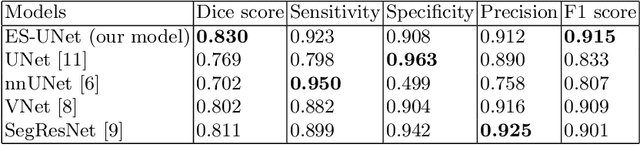
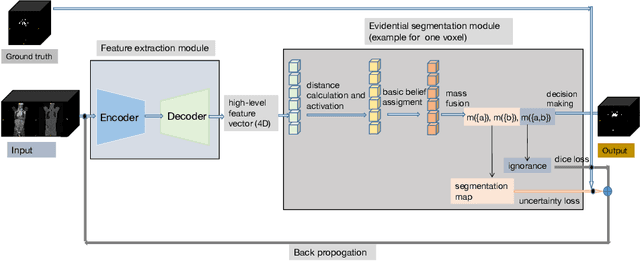
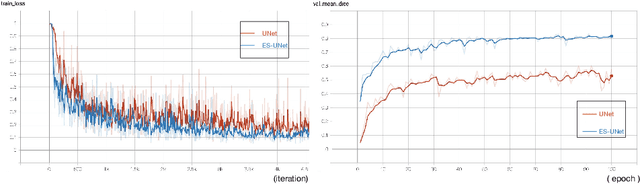
PET and CT are two modalities widely used in medical image analysis. Accurately detecting and segmenting lymphomas from these two imaging modalities are critical tasks for cancer staging and radiotherapy planning. However, this task is still challenging due to the complexity of PET/CT images, and the computation cost to process 3D data. In this paper, a segmentation method based on belief functions is proposed to segment lymphomas in 3D PET/CT images. The architecture is composed of a feature extraction module and an evidential segmentation (ES) module. The ES module outputs not only segmentation results (binary maps indicating the presence or absence of lymphoma in each voxel) but also uncertainty maps quantifying the classification uncertainty. The whole model is optimized by minimizing Dice and uncertainty loss functions to increase segmentation accuracy. The method was evaluated on a database of 173 patients with diffuse large b-cell lymphoma. Quantitative and qualitative results show that our method outperforms the state-of-the-art methods.