Markovian Gaussian Process Variational Autoencoders

Deep generative models are widely used for modelling high-dimensional time series, such as video animations, audio and climate data. Sequential variational autoencoders have been successfully considered for many applications, with many variant models relying on discrete-time methods and recurrent neural networks (RNNs). On the other hand, continuous-time methods have recently gained attraction, especially in the context of irregularly-sampled time series, where they can better handle the data than discrete-time methods. One such class are Gaussian process variational autoencoders (GPVAEs), where the VAE prior is set as a Gaussian process (GPs), allowing inductive biases to be explicitly encoded via the kernel function and interpretability of the latent space. However, a major limitation of GPVAEs is that it inherits the same cubic computational cost as GPs. In this work, we leverage the equivalent discrete state space representation of Markovian GPs to enable a linear-time GP solver via Kalman filtering and smoothing. We show via corrupt and missing frames tasks that our method performs favourably, especially on the latter where it outperforms RNN-based models.

Causal discovery from conditionally stationary time-series

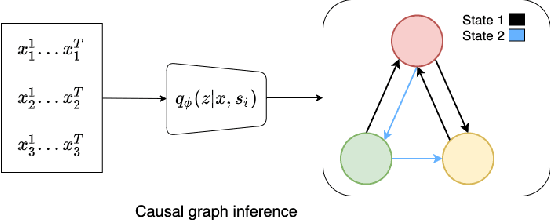
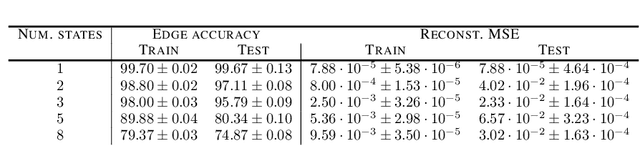
Causal discovery, i.e., inferring underlying cause-effect relationships from observations of a scene or system, is an inherent mechanism in human cognition, but has been shown to be highly challenging to automate. The majority of approaches in the literature aiming for this task consider constrained scenarios with fully observed variables or data from stationary time-series. In this work we aim for causal discovery in a more general class of scenarios, scenes with non-stationary behavior over time. For our purposes we here regard a scene as a composition objects interacting with each other over time. Non-stationarity is modeled as stationarity conditioned on an underlying variable, a state, which can be of varying dimension, more or less hidden given observations of the scene, and also depend more or less directly on these observations. We propose a probabilistic deep learning approach called State-Dependent Causal Inference (SDCI) for causal discovery in such conditionally stationary time-series data. Results in two different synthetic scenarios show that this method is able to recover the underlying causal dependencies with high accuracy even in cases with hidden states.