A Targeted Accuracy Diagnostic for Variational Approximations

Variational Inference (VI) is an attractive alternative to Markov Chain Monte Carlo (MCMC) due to its computational efficiency in the case of large datasets and/or complex models with high-dimensional parameters. However, evaluating the accuracy of variational approximations remains a challenge. Existing methods characterize the quality of the whole variational distribution, which is almost always poor in realistic applications, even if specific posterior functionals such as the component-wise means or variances are accurate. Hence, these diagnostics are of practical value only in limited circumstances. To address this issue, we propose the TArgeted Diagnostic for Distribution Approximation Accuracy (TADDAA), which uses many short parallel MCMC chains to obtain lower bounds on the error of each posterior functional of interest. We also develop a reliability check for TADDAA to determine when the lower bounds should not be trusted. Numerical experiments validate the practical utility and computational efficiency of our approach on a range of synthetic distributions and real-data examples, including sparse logistic regression and Bayesian neural network models.

A Spectral Representation of Kernel Stein Discrepancy with Application to Goodness-of-Fit Tests for Measures on Infinite Dimensional Hilbert Spaces

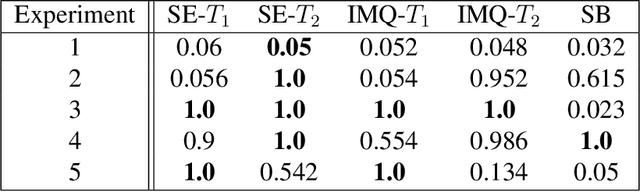
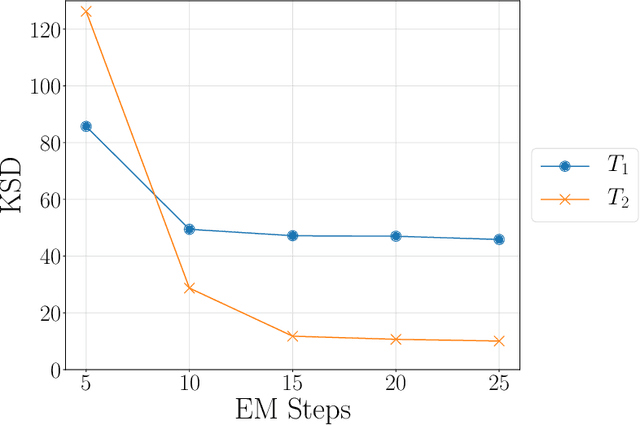
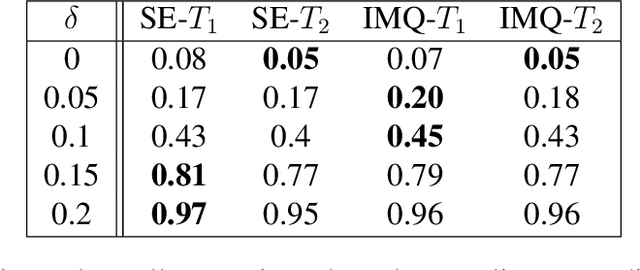
Kernel Stein discrepancy (KSD) is a widely used kernel-based non-parametric measure of discrepancy between probability measures. It is often employed in the scenario where a user has a collection of samples from a candidate probability measure and wishes to compare them against a specified target probability measure. A useful property of KSD is that it may be calculated with samples from only the candidate measure and without knowledge of the normalising constant of the target measure. KSD has been employed in a range of settings including goodness-of-fit testing, parametric inference, MCMC output assessment and generative modelling. Two main issues with current KSD methodology are (i) the lack of applicability beyond the finite dimensional Euclidean setting and (ii) a lack of clarity on what influences KSD performance. This paper provides a novel spectral representation of KSD which remedies both of these, making KSD applicable to Hilbert-valued data and revealing the impact of kernel and Stein operator choice on the KSD. We demonstrate the efficacy of the proposed methodology by performing goodness-of-fit tests for various Gaussian and non-Gaussian functional models in a number of synthetic data experiments.

Practical Posterior Error Bounds from Variational Objectives

Variational inference has become an increasingly attractive fast alternative to Markov chain Monte Carlo methods for approximate Bayesian inference. However, a major obstacle to the widespread use of variational methods is the lack of post-hoc accuracy measures that are both theoretically justified and computationally efficient. In this paper, we provide rigorous bounds on the error of posterior mean and uncertainty estimates that arise from full-distribution approximations, as in variational inference. Our bounds are widely applicable as they require only that the approximating and exact posteriors have polynomial moments. Our bounds are computationally efficient for variational inference in that they require only standard values from variational objectives, straightforward analytic calculations, and simple Monte Carlo estimates. We show that our analysis naturally leads to a new and improved workflow for variational inference. Finally, we demonstrate the utility of our proposed workflow and error bounds on a real-data example with a widely used multilevel hierarchical model.

Scalable Gaussian Process Inference with Finite-data Mean and Variance Guarantees

Gaussian processes (GPs) offer a flexible class of priors for nonparametric Bayesian regression, but popular GP posterior inference methods are typically prohibitively slow or lack desirable finite-data guarantees on quality. We develop an approach to scalable approximate GP regression with finite-data guarantees on the accuracy of pointwise posterior mean and variance estimates. Our main contribution is a novel objective for approximate inference in the nonparametric setting: the preconditioned Fisher (pF) divergence. We show that unlike the Kullback--Leibler divergence (used in variational inference), the pF divergence bounds the 2-Wasserstein distance, which in turn provides tight bounds the pointwise difference of the mean and variance functions. We demonstrate that, for sparse GP likelihood approximations, we can minimize the pF divergence efficiently. Our experiments show that optimizing the pF divergence has the same computational requirements as variational sparse GPs while providing comparable empirical performance--in addition to our novel finite-data quality guarantees.

Practical bounds on the error of Bayesian posterior approximations: A nonasymptotic approach

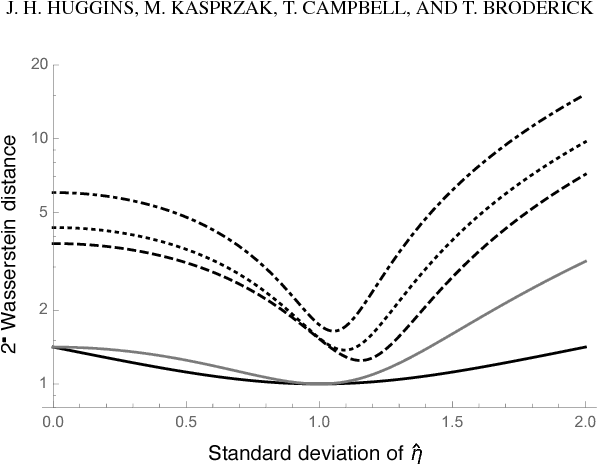
Bayesian inference typically requires the computation of an approximation to the posterior distribution. An important requirement for an approximate Bayesian inference algorithm is to output high-accuracy posterior mean and uncertainty estimates. Classical Monte Carlo methods, particularly Markov Chain Monte Carlo, remain the gold standard for approximate Bayesian inference because they have a robust finite-sample theory and reliable convergence diagnostics. However, alternative methods, which are more scalable or apply to problems where Markov Chain Monte Carlo cannot be used, lack the same finite-data approximation theory and tools for evaluating their accuracy. In this work, we develop a flexible new approach to bounding the error of mean and uncertainty estimates of scalable inference algorithms. Our strategy is to control the estimation errors in terms of Wasserstein distance, then bound the Wasserstein distance via a generalized notion of Fisher distance. Unlike computing the Wasserstein distance, which requires access to the normalized posterior distribution, the Fisher distance is tractable to compute because it requires access only to the gradient of the log posterior density. We demonstrate the usefulness of our Fisher distance approach by deriving bounds on the Wasserstein error of the Laplace approximation and Hilbert coresets. We anticipate that our approach will be applicable to many other approximate inference methods such as the integrated Laplace approximation, variational inference, and approximate Bayesian computation