A Kernel Two-Sample Test for Functional Data

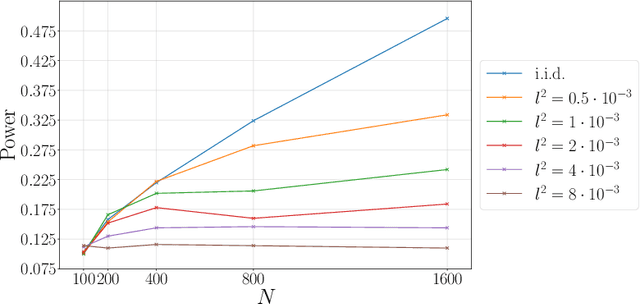
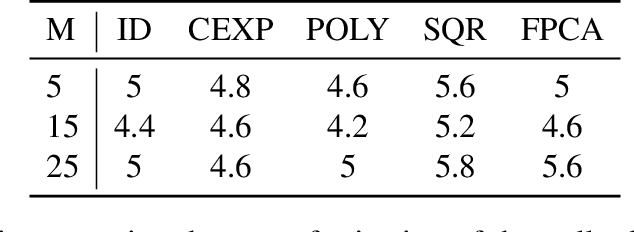
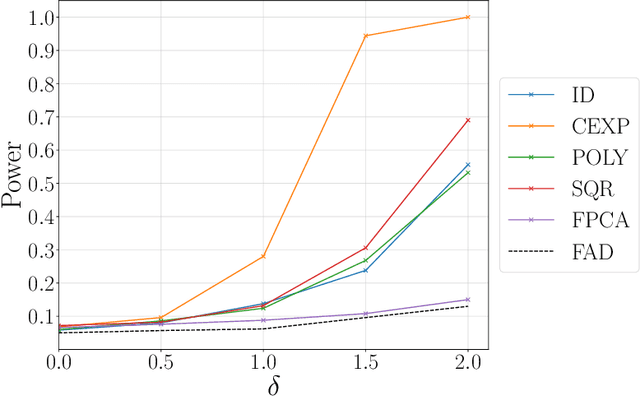
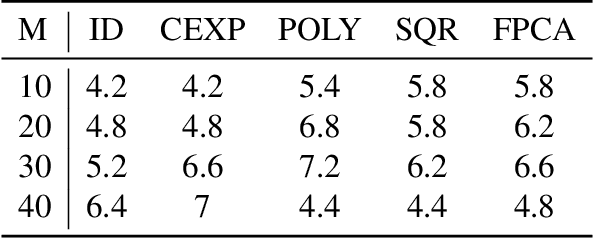
We propose a nonparametric two-sample test procedure based on Maximum Mean Discrepancy (MMD) for testing the hypothesis that two samples of functions have the same underlying distribution, using a kernel defined on a function space. This construction is motivated by a scaling analysis of the efficiency of MMD-based tests for datasets of increasing dimension. Theoretical properties of kernels on function spaces and their associated MMD are established and employed to ascertain the efficacy of the newly proposed test, as well as to assess the effects of using functional reconstructions based on discretised function samples. The theoretical results are demonstrated over a range of synthetic and real world datasets.