Data Driven Density Functional Theory: A case for Physics Informed Learning
Paper and Code
Oct 07, 2020
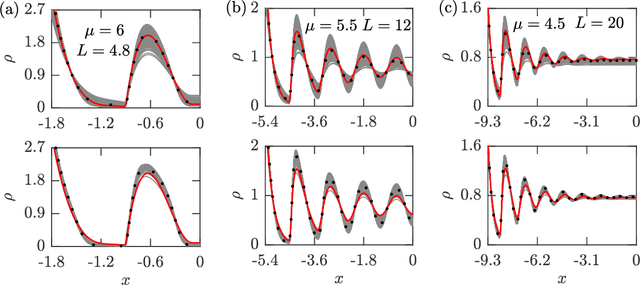

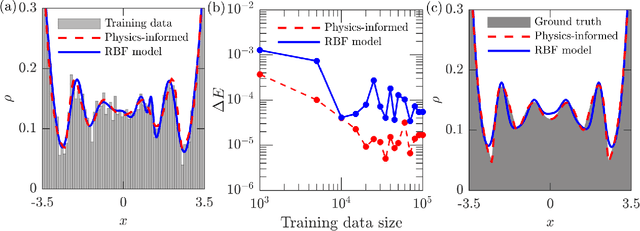
We propose a novel data-driven approach to solving a classical statistical mechanics problem: given data on collective motion of particles, characterise the set of free energies associated with the system of particles. We demonstrate empirically that the particle data contains all the information necessary to infer a free energy. While traditional physical modelling seeks to construct analytically tractable approximations, the proposed approach leverages modern Bayesian computational capabilities to accomplish this in a purely data-driven fashion. The Bayesian paradigm permits us to combine underpinning physical principles with simulation data to obtain uncertainty-quantified predictions of the free energy, in the form of a probability distribution over the family of free energies consistent with the observed particle data. In the present work we focus on classical statistical mechanical systems with excluded volume interactions. Using standard coarse-graining methods, our results can be made applicable to systems with realistic attractive-repulsive interactions. We validate our method on a paradigmatic and computationally cheap case of a one-dimensional fluid. With the appropriate particle data, it is possible to learn canonical and grand-canonical representations of the underlying physical system. Extensions to higher-dimensional systems are conceptually straightforward.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge