Deep Optimal Sensor Placement for Black Box Stochastic Simulations

Selecting cost-effective optimal sensor configurations for subsequent inference of parameters in black-box stochastic systems faces significant computational barriers. We propose a novel and robust approach, modelling the joint distribution over input parameters and solution with a joint energy-based model, trained on simulation data. Unlike existing simulation-based inference approaches, which must be tied to a specific set of point evaluations, we learn a functional representation of parameters and solution. This is used as a resolution-independent plug-and-play surrogate for the joint distribution, which can be conditioned over any set of points, permitting an efficient approach to sensor placement. We demonstrate the validity of our framework on a variety of stochastic problems, showing that our method provides highly informative sensor locations at a lower computational cost compared to conventional approaches.

Physics-informed Bayesian inference of external potentials in classical density-functional theory

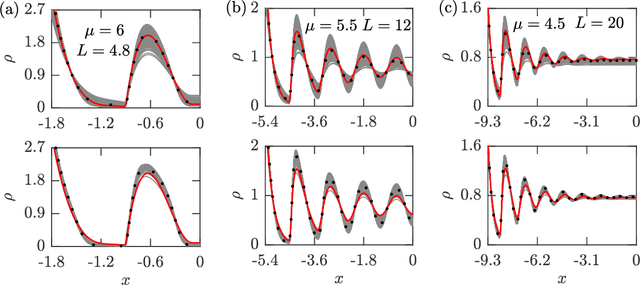
The swift progression of machine learning (ML) has not gone unnoticed in the realm of statistical mechanics. ML techniques have attracted attention by the classical density-functional theory (DFT) community, as they enable discovery of free-energy functionals to determine the equilibrium-density profile of a many-particle system. Within DFT, the external potential accounts for the interaction of the many-particle system with an external field, thus, affecting the density distribution. In this context, we introduce a statistical-learning framework to infer the external potential exerted on a many-particle system. We combine a Bayesian inference approach with the classical DFT apparatus to reconstruct the external potential, yielding a probabilistic description of the external potential functional form with inherent uncertainty quantification. Our framework is exemplified with a grand-canonical one-dimensional particle ensemble with excluded volume interactions in a confined geometry. The required training dataset is generated using a Monte Carlo (MC) simulation where the external potential is applied to the grand-canonical ensemble. The resulting particle coordinates from the MC simulation are fed into the learning framework to uncover the external potential. This eventually allows us to compute the equilibrium density profile of the system by using the tools of DFT. Our approach benchmarks the inferred density against the exact one calculated through the DFT formulation with the true external potential. The proposed Bayesian procedure accurately infers the external potential and the density profile. We also highlight the external-potential uncertainty quantification conditioned on the amount of available simulated data. The seemingly simple case study introduced in this work might serve as a prototype for studying a wide variety of applications, including adsorption and capillarity.

Data Driven Density Functional Theory: A case for Physics Informed Learning

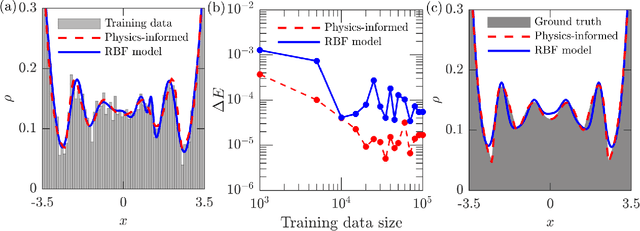
We propose a novel data-driven approach to solving a classical statistical mechanics problem: given data on collective motion of particles, characterise the set of free energies associated with the system of particles. We demonstrate empirically that the particle data contains all the information necessary to infer a free energy. While traditional physical modelling seeks to construct analytically tractable approximations, the proposed approach leverages modern Bayesian computational capabilities to accomplish this in a purely data-driven fashion. The Bayesian paradigm permits us to combine underpinning physical principles with simulation data to obtain uncertainty-quantified predictions of the free energy, in the form of a probability distribution over the family of free energies consistent with the observed particle data. In the present work we focus on classical statistical mechanical systems with excluded volume interactions. Using standard coarse-graining methods, our results can be made applicable to systems with realistic attractive-repulsive interactions. We validate our method on a paradigmatic and computationally cheap case of a one-dimensional fluid. With the appropriate particle data, it is possible to learn canonical and grand-canonical representations of the underlying physical system. Extensions to higher-dimensional systems are conceptually straightforward.